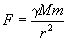 , (3)
, (3)УДК. 12:531.18+51]
Масса покоя или инертная масса?
Р. И. Храпко
Исключение из современных учебников физики инертной массы и замена ее массой покоя представляется ошибкой. Эта тема была поднята автором в статье [1,2]. Здесь приведены дополнительные рассуждения в подтверждение такого тезиса.
Конец 20-го века ознаменовался великой путаницей с физическим понятием "масса тела".
1. Масса покоя
В начале века, до создания теории относительности, было все ясно. Массой тела, m, называлось количество вещества тела, и в то же время масса являлась мерой инертности тела. Инертность тела определяет его "количество движения" при заданной скорости v движения, то есть коэффициент пропорциональности в формуле
P = mv. (1)
P - количество движения или, по-научному, импульс тела, а коэффициент m называется инертной массой.
Но массу как меру инертности тела можно определять и с помощью формулы
F = ma: (2)
чем больше масса, тем меньше ускорение тела при заданной силе. Значение массы по формулам (1) и (2) получалось одно и то же, потому что формула (2) является следствием формулы (1), если инертная масса не зависит от времени и скорости.
То же значение массы можно было получить, взвесив тело, то есть измерив силу притяжения к земле или к любому другому заданному телу (масса которого обозначена M). В законе тяготения Ньютона фигурирует та же самая масса m,
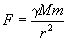 , (3)
, (3)
но тут она называется гравитационной (пассивной) массой. В этом выражается эквивалентность инертной и гравитационной массы. Благодаря этой эквивалентности ускорение свободного падения, как известно, не зависит от природы и массы тела:
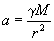 (4)
(4)
2. Инертная масса
Однако при создании теории относительности выяснилось, что никакое тело нельзя разогнать до скорости света, потому что при приближении скорости тела к скорости света ускорение тела уменьшается до нуля, как бы ни была велика ускоряющая сила. Другими словами, выяснилось, что инертность тела возрастает до бесконечности при приближении его скорости к скорости света, хотя "количество вещества" тела, очевидно, остается при этом неизменным.
Выскажемся точнее по поводу увеличения инертности тела. Теория относительности показала, что импульс тела P при любых скоростях остается параллелен скорости v. Поэтому формулу P = mv можно сохранить неизменной при больших скоростях, если принять, что коэффициент m, то есть инертная масса, увеличивается с ростом скорости по закону
![]() , (5)
, (5)
то есть для импульса тела справедливо выражение
![]() . (6)
. (6)
В этих формулах m0 - это то значение массы
рассматриваемого тела, о котором говорилось
вначале, то есть значение, которое можно получить
после того, как тело затормозят до достаточно
малой скорости. Его называют массой покоя тела.
Поэтому формулы (1), (2), (3) следовало бы записать
так: P = m0v, F = m0a,
![]() .
Однако для малых скоростей, как видно из формулы
(5), инертная масса равна массе покоя, m = m0, и поэтому запись (1), (2), (3) в разделе
"до теории относительности" корректна.
.
Однако для малых скоростей, как видно из формулы
(5), инертная масса равна массе покоя, m = m0, и поэтому запись (1), (2), (3) в разделе
"до теории относительности" корректна.
Для того, чтобы подчеркнуть, что инертная масса m зависит от скорости, ее называют иногда "релятивистской" массой: она оказывается различной с точки зрения различных наблюдателей, если эти наблюдатели движутся друг относительно друга. Однако существует выделенное значение инертной массы, именно, значение, которое наблюдает неподвижный относительно тела наблюдатель. Другими словами, масса покоя является выделенным значением инертной массы. Такое свойство инертной массы аналогично свойству времени: одни и те же часы имеют разную скорость хода с точки зрения различных наблюдателей. Однако существует собственная скорость хода часов.
При желании проверить формулу (6) вы должны измерить скорость v тела, а потом измерить импульс тела. Для этого следует затормозить тело некоторой преградой, все время замеряя силу F(t), с которой при торможении тело будет действовать на преграду, а потом проинтегрировать. Импульс, как известно, равен
![]() (7)
(7)
Эта процедура, по сути, задает операционное определение инертной массы.
Заметим, что формулы (5) и (6) остаются справедливыми и для объекта, у которого нет массы покоя, m0 = 0, например, для фотона или нейтрино (если предположить, что масса покоя нейтрино равна нулю). Такие объекты обладают инертной массой и импульсом, но должны двигаться со скоростью света, их нельзя остановить, они исчезают при остановке. Тем не менее, несмотря на постоянство скорости движения, величина их инертной массы оказывается различной с точки зрения различных наблюдателей. Однако в этом случае не существует какого либо выделенного значения инертной массы. Либо, можно сказать, выделенное значение равно нулю.
Увеличение инертности тела при больших скоростях мы объяснили уменьшением ускорения при большой скорости. При этом мы сослались на формулу (2). И это допустимо. Однако именно в силу увеличения инертной массы с ростом скорости тела формула (2) при некоторых условиях изменяет свой вид. Это объясняется тем, что при фиксированном ускорении сила, если она имеет составляющую вдоль скорости, должна обеспечить не только возрастание скорости уже имеющейся массы
![]() , (5)
, (5)
она должна обеспечить возрастание самой массы:
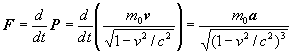 . (8)
. (8)
Коэффициент
![]()
называют иногда продольной массой [3] .
Если сила перпендикулярна скорости и, значит, не изменяет величину скорости и инертной массы, то формула F = ma сохраняет свой вид:
![]() . (9)
. (9)
Последнее обстоятельство позволило Р. Фейнману предложить простой способ операционного определения инертной массы, основанный на формуле (9) и справедливый для любой скорости. "Массу можно измерить так: просто привязать предмет на веревочке, крутить его с определенной скоростью и измерять ту силу, которая необходима, чтобы удержать его." [4]
При произвольном направлении силы
относительно скорости тела коэффициент
пропорциональности в формуле (2) следует
рассматривать как некий оператор (тензор),
превращающий вектор a
в вектор F: F =  a. Оператор
a. Оператор  зависит от величины и
направления скорости тела и, вообще говоря,
изменяет направление вектора. Это нетрудно
принять. Ведь скорость v тела является его свойством, а сила F, действующая на тело - это внешний по
отношению к телу фактор. Понятно, что результат
воздействия силы, то есть ускорение a тела, может зависеть от соотношения
направлений векторов F
и v.
зависит от величины и
направления скорости тела и, вообще говоря,
изменяет направление вектора. Это нетрудно
принять. Ведь скорость v тела является его свойством, а сила F, действующая на тело - это внешний по
отношению к телу фактор. Понятно, что результат
воздействия силы, то есть ускорение a тела, может зависеть от соотношения
направлений векторов F
и v.
3. Гравитационная масса
Одновременно теория относительности показала, что не только инертность тела, но и его вес увеличивается с ростом скорости, причем по тому же закону (5) в соответствии с эквивалентностью инертной и гравитационной массы. Поэтому формула (8) для тела, падающего вниз со скоростью v, выглядит, грубо говоря, так:
![]() =
= ![]() .
.
Точная формула для ускорения может быть получена в рамках общей теории относительности, как показано в конце статьи:
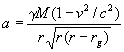 ,
, ![]() . (10)
. (10)
Эта формула является релятивистским аналогом формулы (4).
4. Энергия
Теория относительности показала далее, что прирост инертной массы, m - m0, умноженный на квадрат скорости света, равен как раз кинетической энергии тела:
(m √ m0)c2 = Ek. (11)
Поэтому, если приписать покоящемуся телу энергию покоя E0 = m0c2, то полная энергия E = E0 + Ek тела оказывается пропорциональной инертной массе:
E = mc2 (12)
Эта знаменитая формула Эйнштейна провозглашает эквивалентность инертной массы и энергии. Два, доселе различных понятия, соединяются в одно.
Заметим, что формула (12), как и формулы (5) и (6) остается справедлива и для объекта, у которого нет массы и энергии покоя, m0 = 0.
При желании проверить формулу (11) и одновременно убедиться в справедливости теории относительности вы должны измерить инертную массу и массу покоя тела как было объяснено выше, и, кроме того, измерить кинетическую энергию тела. Для этого следует при торможении тела упомянутой преградой все время замерять силу, с которой тело будет действовать на преграду в процессе торможения в функции перемещения l преграды, F(l), а потом проинтегрировать. Кинетическая энергия, равная, как известно, в данном случае работе, вычисляется по формуле
![]() .
.
Здесь F(l)dl - скалярное произведение силы на инфинитезимальный вектор смещения преграды. Все это рассказано в [5] .
Формула (11) связывает инертную массу, массу покоя и кинетическую энергию. Используя формулу (6) для вычисления разности m2 √ P2/c2, легко связать инертную массу, массу покоя и импульс:
![]() . (13)
. (13)
Для частиц с нулевой массой покоя получаем mc = P или E = Pc.
5. Система тел
При объединении нескольких тел в систему тел, как известно, их импульсы и их инертные массы складываются. Для двух тел это выглядит так:
P = P1 + P2, m = m1 + m2. (14)
Другими словами, импульс и инертная масса аддитивны. Не так обстоит дело с массой покоя. Из формул (13), (14) следует, что масса покоя пары тел с массами покоя m01, m02 равна не сумме m01 + m02, а сложному выражению, зависящему от импульсов P1, P2:
![]() . (15)
. (15)
Таким образом, масса покоя, вообще говоря, не аддитивна. Например, пара фотонов, не имеющих массу покоя, имеет массу покоя, если фотоны летят в разные стороны, и не имеет массу покоя, если фотоны летят в одну и ту же сторону.
Тем не менее, все три величины, P, m, m0, подчиняются закону сохранения, то есть не изменяются со временем для замкнутой системы.
Однако ввиду неаддитивности массы покоя, на наш взгляд, нецелесообразно рассматривать массу покоя системы тел. Имеет смысл говорить лишь о сумме масс покоя отдельных тел системы. В действительности именно так поступают на практике. Когда говорят, что при неупругих соударениях увеличивается масса покоя, имеют ввиду не массу покоя системы, которая удивительным образом сохраняется неизменной при соударениях благодаря неаддитивности, а сравнивают именно сумму масс покоя тел до столкновения и массу покоя после столкновения. Точно так же, когда говорят о дефекте массы покоя при ядерных реакциях, имеют в виду не массу покоя, определяемую формулой (15), а сумму масс покоя частей системы.
6. Сравнение масс
Теперь уместно задать вопрос. Какую из двух масс, массу покоя или инертную массу следует назвать простым словом масса, обозначить буквой m без индексов и тем самым признать "главной" массой. Это - не терминологическая проблема. Здесь имеется серьезная психологическая подоплека.
Чтобы решить, какая из масс - главная, перечислим еще раз свойства обеих масс.
Масса покоя является постоянной величиной для данного тела и выражает "количество вещества тела". Она соответствует привычному дорелятивисткому ньютоновскому представлению о массе. Но она не эквивалентна энергии, не эквивалентна гравитационной массе, она не аддитивна и поэтому не используется как характеристика системы тел или частиц. Это последнее обстоятельство вызывает путаницу (см. [1] , стр. 1365) и мешает проявлению закона сохранения массы покоя. Фотоны и частицы, движущиеся со скоростью света, не обладают массой покоя. Операционное определение массы покоя частицы предполагает торможение ее до малой скорости без использования информации о текущем состоянии частицы.
Инертная масса это - релятивистская масса. Она принимает различное значение для различных наблюдателей, аналогично тому, как скорость хода часов оказывается различной относительно различных наблюдателей. Инертная масса эквивалентна энергии и гравитационной массе, она аддитивна и подчиняется закону сохранения. Инертной массой обладают частицы, не имеющие массы покоя. Операционное определение инертной массы основано на простой формуле P = mv.
На наш взгляд, инертную массу следует называть массой и обозначать m, как это и делалось в настоящей статье.
7. Психологическая подоплека
К сожалению, большое количество физиков считает массу покоя главной и обозначает ее m а не m0, а инертную массу дискриминирует и оставляет без обозначения, что вносит дополнительную путаницу, поскольку из-за этого порой бывает трудно понять, о какой массе идет речь.
Эти физики соглашаются, например, с тем, что масса газа увеличивается при нагревании, потому что увеличивается содержащаяся в нем энергия, но психологический барьер мешает им попросту объяснить это увеличение ростом массы отдельных молекул вследствие увеличения их тепловой скорости.
Эти физики жертвуют представлением о массе как мере инертности в пользу ярлыка, прикрепляемого к каждой частице с информацией о неизменном "количестве вещества", потому что ярлык соответствует их привычному ньютоновскому представлению о массе. Они считают, например, что излучение, которое, согласно Эйнштейну [6] , "переносит инерцию между излучающими и поглощающими телами", не имеет массы, поскольку к излучению невозможно прикрепить ярлык.
Инертная масса отсутствует в издаваемых сейчас стандартных учебниках физики в России (И.В.Савельев) и за рубежом [7,8], а также в популярной литературе [9] . Этот факт, однако, скрыт тем обстоятельством, что сторонники массы покоя настойчиво называют массу покоя не массой покоя, а просто массой, словом, которое ассоциируется с мерой инерции.
Главная психологическая трудность заключается в том, чтобы отождествить массу и энергию (которая изменяется), чтобы принять эти две сущности, как одну. Легко принять формулу E0 = m0c2 для покоящегося тела. Труднее принять справедливость формулы E = mc2 для любой скорости. Замечательная формула E= mc2 представляется, например, Л.Б. Окуню "безобразной" [10] .
Сторонники массы покоя, видимо, не в состоянии
принять идею инертной, релятивистской массы так
же, как ранее противники теории относительности
не могли принять относительность времени. Ведь
время жизни астронавта или нестабильной частицы
изменяется так же, как изменяется их инертная
масса: ![]() . Здесь уместно процитировать М.
Планка: "Великая научная идея редко внедряется
путем постепенного убеждения и обращения своих
противников, редко бывает, что Савл становится
Павлом. В действительности дело происходит так,
что оппоненты постепенно вымирают, а растущее
поколение с самого начала осваивается с новой
идеей." [11] К сожалению, великая идея
релятивистской массы тщательно изолируется от молодежи. На данный момент статья
[1, 2] отклонена редакциями следующих журналов:
"Известия вузов. Физика", "Квант", "American Journal of Physics",
"Physics Education" (Bristol), "Physics Today".
. Здесь уместно процитировать М.
Планка: "Великая научная идея редко внедряется
путем постепенного убеждения и обращения своих
противников, редко бывает, что Савл становится
Павлом. В действительности дело происходит так,
что оппоненты постепенно вымирают, а растущее
поколение с самого начала осваивается с новой
идеей." [11] К сожалению, великая идея
релятивистской массы тщательно изолируется от молодежи. На данный момент статья
[1, 2] отклонена редакциями следующих журналов:
"Известия вузов. Физика", "Квант", "American Journal of Physics",
"Physics Education" (Bristol), "Physics Today".
8. Шварцшильдовское пространство
Мы получим здесь формулу (10), рассмотрев пространство-время Шварцшильда общей теории относительности с выражением для интервала s [12] :
![]() .
.
Уравнения радиальной геодезической
линии могут быть получены по общей формуле,
использующей коэффициенты связности
![]() , (16)
, (16)
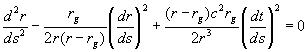 . (17)
. (17)
Первый интеграл уравнения (16) легко находится:
![]() . (18)
. (18)
Запишем теперь выражение для
ускорения a, учитывая (18) и
то, что соотношения между расстоянием l и временем ![]() , с одной стороны, и
координатами r, t, с
другой, даются формулами
, с одной стороны, и
координатами r, t, с
другой, даются формулами
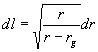 ,
, ![]() :
:
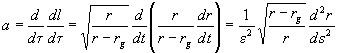 .
.
Выразив таким образом ускорение a через ![]() , мы можем теперь
воспользоваться уравнением (17), а затем,
вернувшись к l и
, мы можем теперь
воспользоваться уравнением (17), а затем,
вернувшись к l и ![]() ,
получить окончательно
,
получить окончательно
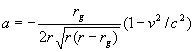 ,
, ![]() . (10)
. (10)
Список литературы
1. Храпко Р. И. Что есть масса? // Успехи физических наук. - 2000, N12. √ с.1363-1366.
2. Храпко Р. И. Что есть масса? - http://www.mai.ru. Труды МАИ, Вып.2.
3. Фриш С. Э., Тиморева А. В. Курс общей физики. Т. 3. - М.: ГИТТЛ, 1951.- 547 с.
4. Фейнман Р. и др. Фейнмановские лекции по физике. Т. 1. - М.: Мир, 1965. √ 232 с.
5. Храпко Р. И., Спирин Г.Г., Разоренов В. М. Механика. - М.: МАИ, 1993. √ 89 с.
6. Эйнштейн А. Зависит ли инерция тела от содержащейся в нем энергии. // Принцип относительности. - ОНТИ, 1935.- с.175-178.
7. Resnick R., Halliday D., Krane K. S. Physics. V.1 - N.Y.: J. Wiley, 1992.-592p.
8. Alonso M., Finn E. J. Physics - N.Y.: Addison-Wesley, 1995.-496p.
9. Taylor E. F., Wheeler J. A. Spacetime Physics. √ San Francisco: Freeman, 1966.- 631c. Русский перевод: Тейлор Э. Ф., Уилер Дж. А. Физика пространства-времени. √ М.: Мир, 1971.- 612c.
10. Окунь Л. Б. Понятие массы. // Успехи физических наук. - 1989, т. 158. - с.512-530.
11. Планк М. Происхождение научных идей и влияние их на развитие науки./ М. Планк.// Сборник статей к столетию со дня рождения Макса Планка. - М.: АНСССР, 1958.- с.52.
12. Ландау Л.Д., Лифшиц Е.М. Теория поля. - М.: Наука, 1973.- 504с.