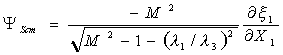За рубежом значительное внимание уделяется выявлению основных механизмов, определяющих возникновение на поверхности головной части летательного аппарата (ЛА) упорядоченной рельефной структуры. Практический интерес к этому явлению связан с тем влиянием, которое оно оказывает на температуру поверхности и динамику полета ЛА.

Установлено, что ромбическая рельефная структура поверхности реактивного сопла и корпуса ЛА может вызывать вращение ЛА относительно оси крена [1]. Было также установлено, что рельефная сетка [2] образуется пересекающимися спиральными канавками с правым и левым направлениями спирали на поверхности тела и угол наклона спирали (волновой угол) зависит от числа Маха на границе пограничного слоя. Была также выявлена связь между изменением длины волны рельефной структуры поверхности и давлением потока, а также между изменением шага рельефной сетки в направлении течения и поверхностным трением.

В настоящей работе рассмотрена простая модель волнистой поверхности в виде плоской панели, имеющей ромбическую рельефную структуру в виде периодически повторяющихся выступов и впадин. Переход от осесимметричной оболочки сопла и головной части ЛА к плоской панели возможен вследствие малости смещения его контура от исходного теоретического профиля относительно расстояния от оси << 1.
Расчетная модель рельефа поверхности образуется синусоидальными кривыми.

Распространение малых возмущений давления , и других параметров однородного потока газа, обтекающего плоскую панель с рельефной структурой поверхности со скоростью V по оси Х , описывается уравнением Блохинцева [3]:

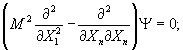    (1)

где - безразмерная переменная для возмущения давления, которая равна ; здесь Р - давление газа; k - отношение удельных теплоемкостей; число Маха
- квадрат скорости звука, - плотность газа.

Граничное условие для газа на волнистой поверхности оболочки сопла должно отображать повсеместный контакт газа с обтекаемой поверхностью стенки сопла. Для этого необходимо, чтобы производная поперечного смещения панели по нормали к вектору скорости V потока равнялась относительной составляющей возмущенной скорости по тому же направлению .

Откуда с помощью линеаризованного уравнения движения по - направлению получим граничное условие на рельефной поверхности стенки при в виде [4]:

;      (2)

Смещение поверхности плоской панели при представим в общем случае комплексным выражением

    (3)

Решение задачи об обтекании потоком этой рельефной поверхности панели будем искать с помощью метода Фурье в виде двух групп плоских волн:

    (4)

Представив каждое из слагаемых в уравнение (1) и выразив через и

найдем семейство разделенных решений:

    (5)

Чтобы решение уравнения (4) удовлетворяло граничному условию (2), подставим в него (3) и (5):

Как видно, чтобы это равенство имело место в каждой точке плоскости , необходимо: и .
Это позволит найти связь между амплитудами смещения стенки и возмущениями газодинамических параметров:

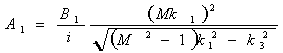
Итак, вызываемые смещениями (3) возмущения газодинамических параметров, удовлетворяющие в поле течения уравнению (1), а на стенке - граничному условию (2), представляются плоскими волнами:

    (6)

где : S = 1, 2; - длина волны возмущения.

Обтекание потоком рельефной поверхности пластинки может быть:

• дозвуковым М<1 и докритическим ;
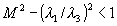• сверхзуковым М>1 и докритическим ;
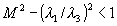• сверхзвуковым М>1 и сверхкритическим .

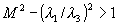Фундаментальные решения (6) при сверхкритическом обтекании имеют значения на стенке, определяемые по формуле:

    (7)

При обращении в нуль знаменателя амплитуды (7) имеет место критический режим обтекания поверхности с рельефной структурой, который при переходит в критический звуковой режим стационарного обтекания: .