УДК 629.7.027

А.В. Трямкин, С.Н. Скиданов

Современный процесс десантирования различной техники и грузов можно разбить на следующие основные этапы:

I-й этап √ вытягивание десантируемого объекта (ДО) из самолета вытяжной парашютной системой (ВПС);

II-й этап √ движение ДО в воздухе;

III-й этап √ приземление ДО.

Основная парашютная система (ОПС) может применяться как в однокупольном варианте, так и в многокупольном варианте, поэтому в дальнейшем, не зависимо от количества парашютов, будем считать ОПС исполненной в однокупольном варианте, т.к. многокупольную систему можно привести к системе с одним парашютом площадью, равной сумме всех площадей парашютов многокупольной системы.

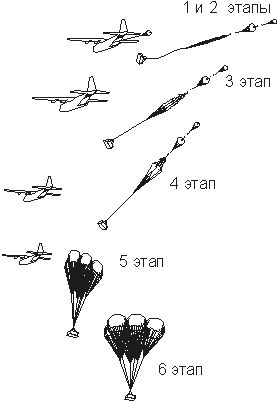
Второй основной этап √ движение десантируемого объекта в воздухе, можно разбить на следующие этапы (рис. 1):

Рис. 1. Этапы движения десантируемого объекта в воздухе.

1-й этап √ отделение дополнительного вытяжного парашюта от ДО и его наполнение.

Продолжительность первого этапа называется временем раскрытия дополнительного вытяжного парашюта . В течение первого этапа изменение скорости ДО и пройденного им пути происходит по законам падения в воздухе тела без парашюта.

2-й этап √ отделение блока с основной парашютной системой от ДО, вытягивание купола (или куполов, в случае применения многокупольной парашютной системы) и строп на всю их длину и стягивание парашютной камеры с купола.

Наполненный воздухом дополнительный вытяжной парашют, быстро теряя скорость, снимает блок основной парашютной системы с ДО, вытягивает стропы из сот парашютной камеры и стаскивает камеру с купола. При этом купол основного парашюта вместе со стропами вытягивается на всю длину.

В течение второго этапа, если пренебречь трением купола при стаскивании парашютной камеры и усилиями, возникающими при выходе строп из сот камеры, изменение скорости падения ДО и длины пройденного им пути (как и в течение первого этапа) происходит по законам падения тела в воздухе без парашюта.

Продолжительность второго этапа зависит от размеров дополнительного вытяжного парашюта, от массы ОПС, от длины купола и строп, от длины парашютной камеры и ее конструкции, скорости падения ДО к концу второго этапа и других факторов.

Как видно, в течение первых двух этапов движения в воздухе, с момента отделения ДО от самолета до полного вытягивания купола и строп на всю длину, парашют как тормозное устройство не работает.

Скорость ДО изменяется незначительно от скорости самолета до скорости в момент введения основного парашюта в действие. Время с момента отделения ДО от самолета до вытягивания купола и строп на всю их длину называется временем вытягивания и обозначается : .

3-й этап √ наполнение купола парашюта до площади ограниченной рифовкой.

В конце второго этапа, после вытягивания купола и строп на всю их длину, начинается наполнение купола парашюта до площади ограниченной рифовкой. Продолжительность третьего этапа называется временем наполнения зарифованного парашюта .

4-й этап √ снижение на зарифованном куполе.

В течение четвертого этапа ДО объект снижается на зарифованном парашюте. Время с момента наполнения зарифованного парашюта до момента разрифовки парашюта называется временем снижения на зарифованном парашюте и обозначается : .

5-й этап √ наполнение купола парашюта.

На пятом этапе происходит разрифовка парашюта. Купол парашюта наполняется до полной площади за время . Время с момента начала наполнения зарифованного купола до его полного раскрытия называется временем наполнения основного парашюта и обозначается : .

6-й этап √ снижение на раскрытом парашюте.

В течение шестого этапа ДО снижается на раскрытом парашюте до достижения им поверхности земли. Как правило, время шестого этапа выбирается таким образом, чтобы перед приземлением система "груз-парашют" имела скорость установившегося снижения.

Много работ как отечественных, так и зарубежных посвящено исследованиям процесса наполнения парашюта /1, 3, 4, 5, 6, 8/, но все они, в основном, решают вопросы связанные с проектированием парашютов и не дают достаточно простых выражений для исследования динамики движения системы "груз-парашют" в процессе наполнения купола.

В процессе наполнения изменяются как площадь купола парашюта , так и его коэффициент сопротивления . Знание законов изменения выше перечисленных параметров позволило бы существенно упростить решение задач связанных с наполнением парашюта. Существует много работ, где даются законы изменения площади парашюта и коэффициента сопротивления, но проще всего искать вид зависимостей изменения площади парашюта и коэффициента сопротивления не отдельно, а в виде их произведения. Это произведение называется эффективной площадью сопротивления парашюта и обозначается :

.      (1)

Анализ экспериментальных исследований процесса наполнения купола в аэродинамической трубе /4/ и проведенных летных испытаний (рис. 2) парашютно-реактивной системы (ПРС) в составе многокупольной парашютной системы МКС-175-12 /7/ позволяет найти зависимость эффективной площади парашюта от времени наполнения t, которую с достаточной степенью точности можно аппроксимировать /2/ кривой

,      (2)

где а √ постоянная величина, значение которой будет найдено ниже; к √ постоянная наполнения √ безразмерная величина, определяется экспериментально, для парашютной системы МКС-175-12 /10/; √ время наполнения парашюта, с.

По результатам летных испытаний, в конце наполнения парашюта коэффициент сопротивления принимает максимальное значение, следовательно, . Эффективная площадь сопротивления парашюта будет равна

откуда

.      (3)

Подставим (3) в (2), окончательно получим зависимость изменения эффективной площади сопротивления парашюта от времени наполнения

.      (4)

В случае использования рифовки эффективная площадь сопротивления от времени наполнения зарифованного парашюта будет иметь вид:

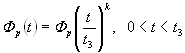     (5)

где √ эффективная площадь сопротивления зарифованного парашюта, м²; √ время наполнения зарифованного парашюта, с.

Изменение эффективной площади сопротивления за время наполнения парашюта после разрифовки определяется из выражения

.      (6)

В конце наполнения парашюта и

откуда

.      (7)

Подставим (7) в (6), окончательно получим

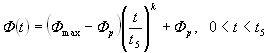.      (8)

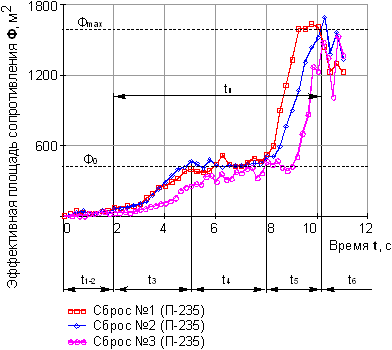
Рис. 2. Изменение эффективной площади сопротивления парашютной системы от времени

Воспользуемся полученными выражениями для определения траекторных параметров существующей серийной парашютно-реактивной системы, движение в воздухе которой происходит в соответствии со всеми выше изложенными этапами.

При составлении уравнений движения системы "груз√парашют" будем предполагать, что при снижении системы ось парашюта, проходящая через коуш строп и вершину купола, касательная к траектории движения груза, а парашют обтекается потоком, скорость которого на бесконечности равна скорости движения груза и совпадает по направлению с осью парашюта. Масса груза намного больше массы парашюта. Пренебрежем возмущениями, вносимыми в поток присутствием груза. Пренебрежем также центробежными силами, действующими на парашют при движении системы по криволинейной траектории. Материал купола и строп будем считать нерастяжимыми, а воздух √ несжимаемым.

Уравнения движения в связанной системе координат, с учетом принятых допущений будут иметь вид:

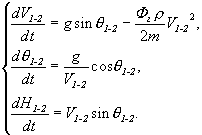(9)

где m √ масса системы, кг; V_1-2 √ скорость центра масс системы, м/с; g √ ускорение свободного падения, м/с²; √ угол наклона траектории, рад; √ эффективная площадь сопротивления груза, м²; √ плотность воздуха у земли, кг/м³; √ потеря высоты на первом этапе. В дальнейшем, индексы, стоящие при переменных, относятся к каждому из рассматриваемых этапов.

Так как в процессе летных испытаний ПРС диапазон высот десантирования составлял 300√400 метров, то в целях упрощения задачи будем считать плотность воздуха постоянной величиной равной плотности на высоте (плотность воздуха у земли отличается от плотности воздуха на высоте 400 м при стандартных атмосферных условиях не более чем на 4%).

Система дифференциальных уравнений (9) интегрируется при начальных условиях: , , , где √ скорость полета самолета, √ высота десантирования. Пределы интегрирования , время вытягивания парашютной системы МКС-175-12 по результатам летных испытаний ПРС равно с.

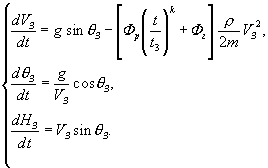     (10)

Система дифференциальных уравнений (10) интегрируется при начальных условиях: , , . Пределы интегрирования .

На основании закона непрерывности парашюты должны раскрываться на определенной длине, т.к. для наполнения купола требуется заданный конический столб воздуха впереди купола. Эта определенная длина пропорциональна номинальному диаметру парашюта. В работе /5/ дается формула для определения времени наполнения парашютов:

,      (11)

где п √ постоянная безразмерная величина, типичная для каждого парашюта, указывающая длину наполнения как кратное значение ; V √ скорость системы "груз-парашют" в момент наполнения купола.

Так по результатам экспериментов десантирования ПРС постоянная п при наполнении зарифованной парашютной системы МКС-175-12 равна , а при наполнении после разрифовки √ .

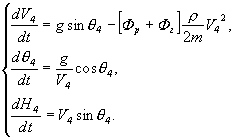     (12)

Система дифференциальных уравнений (12) интегрируется при начальных условиях: , , . Пределы интегрирования .

Время движения системы после наполнения зарифованного парашюта равно √ .

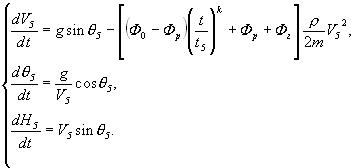     (13)

Система дифференциальных уравнений (13) интегрируется при начальных условиях: , , . Пределы интегрирования . Продолжительность пятого этапа определяется из выражения (11).

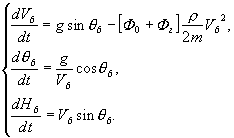     (14)

Система дифференциальных уравнений (14) интегрируется при начальных условиях: , , .

На рисунке 3 даются экспериментальная и теоретическая зависимости изменения скорости снижения ПРС от времени. Интегрирование систем (9√10) и (12-14) проводилось с помощью ЭВМ. Масса ПРС кг; начальная скорость десантирования м/с; высота десантирования м; угол наклона траектории системы в момент отделения от самолета рад; эффективная площадь сопротивления груза м²; эффективная площадь сопротивления парашютной системы м²; эффективная площадь сопротивления зарифованной парашютной системы м²; постоянная наполнения ; постоянная п при наполнении зарифованной парашютной системы МКС-175-12 равна , а при наполнении после разрифовки √ .

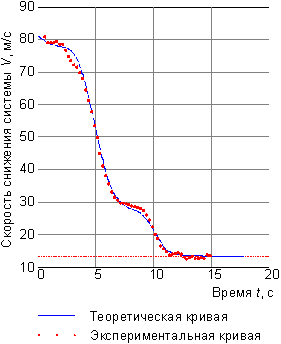
Рис. 3. Изменение скорости снижения системы от времени.

В заключение следует отметить, что найденная зависимость изменения эффективной площади сопротивления парашюта от времени его наполнения позволят существенно упростить решение задач динамики движения системы "груз-парашют", получая при этом достоверные результаты.

1. Белоцерковский С.М., Ништ М. И., Пономарев А. Т., Рысев О. В. Исследование парашютов и дельтапланов на ЭВМ. √ М.: Машиностроение, 1987. √ 240 с.

2. Гутер Р. С., Овчинский Б. В. Элементы численного анализа и математической обработки результатов опыта. √ М.: Наука, 1970. √ 432 с.

3. Морозов В. И., Пономарев А. Т., Рысев О. В. Математическое моделирование сложных аэроупругих систем. √ М.: Физматлит, 1995. √ 736 с.

4. Носарев И. М. Исследование в аэродинамических трубах процесса раскрытия круглого купола парашюта. √ М.: ЦАГИ, 1963. √ 32 с.

5. Нэке Т.В. Руководство по проектированию парашютных спасательных систем. Глава 5. Характеристики и эксплуатационные качества парашютов. √ М.: ЦНТИ "Волна", 1989.√152 с.

6. Рысев О. В., Пономарев А. Т., Васильев М. И., Вишняк А. А., Днепров И. В., Мосеев Ю. В. Парашютные системы. √ М.: Наука, 1996. √ 228 с.

7. Средства десантирования изделия "688". Отчет по результатам предварительных летных испытаний П235-0000 Отч 8. √ МКПК "Универсал", инв. ╧ 7130-90, 1991. √ 28 с.

8. Dennis D.R. Recent advances in parachute technology // The aeronautical journal. √ 1983, V. 87, ╧ 869, P. 333√342.