Одной из актуальных задач управления как поточно-групповым, так и гибким автоматизированным производством является оптимизация расписания рабочих мест заданным объектом, которая алгоритмически сводится к выбору оптимальной очередности запуска партий деталей на различных рабочих местах и относится к классу комбинаторных задач дискретной математики. В настоящее время распространение получили приближенные эвристические методы решения этой задачи, поскольку использованию точных универсальных комбинаторных методов мешают ее большая размерность и нерегулярность целевой функции, не позволяющие строить эффективные оценки частичных решений в алгоритмах, реализующих схему метода ветвей и границ.

На практике в качестве критерия оптимальности решения данной задачи наиболее часто используется минимум длительности совокупного производственного цикла, так как он косвенным образом учитывает большинство показателей, отражающих эффективность процесса производства, в том числе, коэффициент загрузки оборудования, амортизационные отчисления, время межоперационного пролеживания, незавершенное производство. К тому же, реализация этого критерия не требует какой-либо дополнительной информации кроме данных о производственной программе на принятый период и информации, характеризующей технологический процесс обработки.  

С учетом параллельности процессов обработки деталей одной номенклатуры на различных рабочих местах и возникающих при этом смещений времен начала их обработки на подающем и получающем местах [1], длительность совокупного производственного цикла может быть рассчитана только, как разность календарных сроков начала обработки первой по очереди детали на первом рабочем месте и окончания обработки последней детали на последнем рабочем месте:

T = _nm + t_nm      (1)

где T - совокупная продолжительность цикла работ,

_nm - время начала запуска n-й партии деталей на m-м рабочем месте (последней партии на последнем месте;

t_nm - время обработки n-й партии деталей на m-м рабочем месте;

Это означает, что целевая функция сформулированной оптимизационной задачи не может быть выражена единым аналитическим выражением и требует довольно сложного алгоритмического расчета для каждого из альтернативных вариантов загрузки оборудования (очередности обработки деталей на различных рабочих местах). Эти расчеты сводятся в основном к построению графика работ, то есть к последовательному определению времени запуска и завершения обработки каждой партии деталей на каждом рабочем месте. Основным инструментом построения графика работ является математическая модель процесса производства и , таким образом, именно она будет выступать в качестве целевой функции рассматриваемой задачи. Соответственно точность решения также будет определяться точностью этой модели.

Наиболее адекватной реальным производственным процессам является модель с параллельно-последовательной обработкой партий деталей одной номенклатуры на подающей и принимающей позициях. В данной модели время запуска и завершения обработки партии деталей на конкретном рабочем месте следует определять, как максимум из времени завершения обработки передаточной партии деталей рассматриваемой номенклатуры на предыдущем рабочем месте и времени окончания обработки предыдущей партии деталей на рассматриваемом рабочем месте.  

_ij = max { _i,j-1 + t^пп_i,j-1 , _i-1,j + t_i-1,j }     (2)

где _i,j-1 - время начала запуска i-й партии деталей на (j-1)-м рабочем месте;

t^пп_i,j-1 - время обработки передаточной партии i-й детали на (j-1)-м рабочем месте

t_i-1,j - время обработки (i-1)-й партии деталей на j-м рабочем месте.

В случае учета профилактического ремонта оборудования эти времена уточняются. То есть, если срок окончания обработки анализируемой партии деталей превосходит плановое время начала профилактического ремонта, то начало обработки этой партии деталей будет равно времени завершения обработки предыдущей партии на этом рабочем месте плюс время профилактического ремонта:

_ij = max { _i,j-1 + t^пп_i,j-1 , _i-1,j + t_i-1,j } + u_j t^р_j      (3)

где t^р_j - время профилактического ремонта j-го рабочего места;

u_j √ коэффициент, учитывающий необходимость ремонта на j-м рабочем месте.

u_j = 1, если ^р_{j <} max { _i,j-1 + t^пп_i,j-1 , _i-1,j + t_i-1,j } < ^р_j + t^р_j

u_j = 0, в противном случае.

где ^р_j √ плановое время начала ремонта (в часах функционирования оборудования, начиная с запуска первой детали)

Таким образом целевая функция рассматриваемой задачи рассчитывается алгоритмически, что с одной стороны увеличивает время расчетов, а с другой - затрудняет получение оценок ее возможных значений на частичном плане задачи. Точность оценок собственно и определяет эффективность применения точных методов типа ветвей и границ, которые при плохих оценках вырождаются в метод полного перебора. Поднять эффективность этих методов можно не только улучшая точность оценок, но и выбрав в качестве начальной точки поиска хорошее начальное решение.  

В предлагаемом комплексном комбинаторном методе оптимизации расписания работы рабочих мест в качестве начальной точки для применения схемы метода ветвей и границ используются два последовательно применяемых приближенных метода: метод случайного поиска и поиск на перестановочной решетке. Алгоритм метода, таким образом, представляет собой объединение трех автономных алгоритмов формирования расписания с последовательным выполнением каждого из них и передачей полученного оптимального решения от одного алгоритма к другому.

Алгоритм случайного поиска для неизменной очередности партий деталей на различных рабочих местах заключается в следующем. Каждому номеру очереди (кроме последнего) ставится в соответствие непрерывный числовой интервал от 0 до 1. Каждый из интервалов разбивается на число частей, соответствующее числу партий деталей, которые можно поставить в этот номер очереди. То есть, для первого номера очереди - на M частей (поскольку для запуска можно выбирать все детали), для второго номера очереди - на M-1 часть (поскольку для запуска можно выбирать (M-1) деталь - одна из партий деталей уже включена в первую очередь) и так далее, кроме последнего номера очереди, для которого остается только одна, еще не включенная в очередь деталь. Таким образом, для i-го рабочего места интервал разбивается на (M+1-i) частей.

С помощью датчика случайных чисел выбирается случайное число в интервале от 0 до 1, и в очередь включается та деталь, в чью часть (0,1)-го интервала попало это случайное число. Таким образом, для первого номера очереди номер детали будет определяться выражением

x₁ = div(10*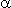 /(1/(M+1-i))) +1      (4)

Для остальных номеров очереди выражение (4) будет определять порядок расположения номера деталей в списке деталей, имеющихся для выбора на i-м номере очереди.

После того, как произойдет выбор детали для первого номера очереди запуска, список деталей, имеющихся для выбора на 2-м номере очереди, определяется, как исходный список минус деталь, выбранная в первую очередь. Список для третьей очереди определяется, как список для второй очереди за исключением детали, выбранной для второй очереди и так далее.

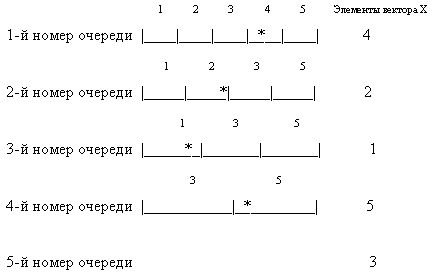
Рис. 1. Схема применения алгоритма случайного поиска определения очередности запуска.