УДК 330.4

Л.И.Кобко

Предлагаемая работа посвящена актуальному вопросу использования математических методов в управлении производственными процессами. Рассматривается задача построения оптимального расписания работы рабочих мест, являющаяся ядром систем оперативного управления поточно-групповым производством. В настоящий момент на практике применяются эвристические методы решения этой задачи, так как в силу ряда ее особенностей точные методы вырождаются в полный перебор вариантов. В работе предлагается новый метод решения, представляющий собой гибридную вычислительную процедуру, где для ускорения сходимости точного метода типа ветвей и границ на определенных шагах его алгоритма используются методы поиска локально-оптимального решения комбинаторных задач.

Одной из актуальных задач управления как поточно-групповым, так и гибким автоматизированным производством является оптимизация расписания рабочих мест заданным объектом, которая алгоритмически сводится к выбору оптимальной очередности запуска партий деталей на различных рабочих местах и относится к классу комбинаторных задач дискретной математики. В настоящее время распространение получили приближенные эвристические методы решения этой задачи, поскольку использованию точных универсальных комбинаторных методов мешают ее большая размерность и нерегулярность целевой функции, не позволяющие строить эффективные оценки частичных решений в алгоритмах, реализующих схему метода ветвей и границ.

На практике в качестве критерия оптимальности решения данной задачи наиболее часто используется минимум длительности совокупного производственного цикла, так как он косвенным образом учитывает большинство показателей, отражающих эффективность процесса производства, в том числе, коэффициент загрузки оборудования, амортизационные отчисления, время межоперационного пролеживания, незавершенное производство. К тому же, реализация этого критерия не требует какой-либо дополнительной информации кроме данных о производственной программе на принятый период и информации, характеризующей технологический процесс обработки.

С учетом параллельности процессов обработки деталей одной номенклатуры на различных рабочих местах и возникающих при этом смещений времен начала их обработки на подающем и получающем местах [1], длительность совокупного производственного цикла может быть рассчитана только, как разность календарных сроков начала обработки первой по очереди детали на первом рабочем месте и окончания обработки последней детали на последнем рабочем месте:

T = _nm + t_nm      (1)

где T - совокупная продолжительность цикла работ,

_nm - время начала запуска n-й партии деталей на m-м рабочем месте (последней партии на последнем месте;

t_nm - время обработки n-й партии деталей на m-м рабочем месте;

Это означает, что целевая функция сформулированной оптимизационной задачи не может быть выражена единым аналитическим выражением и требует довольно сложного алгоритмического расчета для каждого из альтернативных вариантов загрузки оборудования (очередности обработки деталей на различных рабочих местах). Эти расчеты сводятся в основном к построению графика работ, то есть к последовательному определению времени запуска и завершения обработки каждой партии деталей на каждом рабочем месте. Основным инструментом построения графика работ является математическая модель процесса производства и , таким образом, именно она будет выступать в качестве целевой функции рассматриваемой задачи. Соответственно точность решения также будет определяться точностью этой модели.

Наиболее адекватной реальным производственным процессам является модель с параллельно-последовательной обработкой партий деталей одной номенклатуры на подающей и принимающей позициях. В данной модели время запуска и завершения обработки партии деталей на конкретном рабочем месте следует определять, как максимум из времени завершения обработки передаточной партии деталей рассматриваемой номенклатуры на предыдущем рабочем месте и времени окончания обработки предыдущей партии деталей на рассматриваемом рабочем месте.

_ij = max { _i,j-1 + t^пп_i,j-1 , _i-1,j + t_i-1,j }     (2)

где _i,j-1 - время начала запуска i-й партии деталей на (j-1)-м рабочем месте;

t^пп_i,j-1 - время обработки передаточной партии i-й детали на (j-1)-м рабочем месте

t_i-1,j - время обработки (i-1)-й партии деталей на j-м рабочем месте.

В случае учета профилактического ремонта оборудования эти времена уточняются. То есть, если срок окончания обработки анализируемой партии деталей превосходит плановое время начала профилактического ремонта, то начало обработки этой партии деталей будет равно времени завершения обработки предыдущей партии на этом рабочем месте плюс время профилактического ремонта:

_ij = max { _i,j-1 + t^пп_i,j-1 , _i-1,j + t_i-1,j } + u_j t^р_j      (3)

где t^р_j - время профилактического ремонта j-го рабочего места;

u_j √ коэффициент, учитывающий необходимость ремонта на j-м рабочем месте.

u_j = 1, если ^р_{j <} max { _i,j-1 + t^пп_i,j-1 , _i-1,j + t_i-1,j } < ^р_j + t^р_j

u_j = 0, в противном случае.

где ^р_j √ плановое время начала ремонта (в часах функционирования оборудования, начиная с запуска первой детали)

Таким образом целевая функция рассматриваемой задачи рассчитывается алгоритмически, что с одной стороны увеличивает время расчетов, а с другой - затрудняет получение оценок ее возможных значений на частичном плане задачи. Точность оценок собственно и определяет эффективность применения точных методов типа ветвей и границ, которые при плохих оценках вырождаются в метод полного перебора. Поднять эффективность этих методов можно не только улучшая точность оценок, но и выбрав в качестве начальной точки поиска хорошее начальное решение.

В предлагаемом комплексном комбинаторном методе оптимизации расписания работы рабочих мест в качестве начальной точки для применения схемы метода ветвей и границ используются два последовательно применяемых приближенных метода: метод случайного поиска и поиск на перестановочной решетке. Алгоритм метода, таким образом, представляет собой объединение трех автономных алгоритмов формирования расписания с последовательным выполнением каждого из них и передачей полученного оптимального решения от одного алгоритма к другому.

Алгоритм случайного поиска для неизменной очередности партий деталей на различных рабочих местах заключается в следующем. Каждому номеру очереди (кроме последнего) ставится в соответствие непрерывный числовой интервал от 0 до 1. Каждый из интервалов разбивается на число частей, соответствующее числу партий деталей, которые можно поставить в этот номер очереди. То есть, для первого номера очереди - на M частей (поскольку для запуска можно выбирать все детали), для второго номера очереди - на M-1 часть (поскольку для запуска можно выбирать (M-1) деталь - одна из партий деталей уже включена в первую очередь) и так далее, кроме последнего номера очереди, для которого остается только одна, еще не включенная в очередь деталь. Таким образом, для i-го рабочего места интервал разбивается на (M+1-i) частей.

С помощью датчика случайных чисел выбирается случайное число в интервале от 0 до 1, и в очередь включается та деталь, в чью часть (0,1)-го интервала попало это случайное число. Таким образом, для первого номера очереди номер детали будет определяться выражением

x₁ = div(10*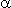 /(1/(M+1-i))) +1      (4)

Для остальных номеров очереди выражение (4) будет определять порядок расположения номера деталей в списке деталей, имеющихся для выбора на i-м номере очереди.

После того, как произойдет выбор детали для первого номера очереди запуска, список деталей, имеющихся для выбора на 2-м номере очереди, определяется, как исходный список минус деталь, выбранная в первую очередь. Список для третьей очереди определяется, как список для второй очереди за исключением детали, выбранной для второй очереди и так далее.

Рис. 1. Схема применения алгоритма случайного поиска определения очередности запуска.

Алгоритм поиска на перестановочном множестве базируется на следующих теоретических соображениях. Задача определения оптимальной очередности запуска деталей относится к группе перестановочных задач комбинаторного программирования [2] , множество решений которых представляет собой так называемый перестановочный многогранник, то есть векторную решетку с возможностью перехода в любое решение за конечное число перестановок. Перестановочный многогранник является матроидом √ комбинаторным множеством, на котором имеет место совпадение локального и глобального оптимумов целевых функций определенного вида. Для того, чтобы локальный и глобальный экстремумы целевой функции совпадали на матроиде, эта функция должна быть дискретно-выпуклой. Дискретно-выпуклой называют функцию дискретных переменных, обладающую свойствами, аналогичными свойству выпуклости целевой функции непрерывных экстремальных задач. На матроиде может быть введено понятие градиента дискретно-выпуклой функции и на его основе получено конструктивное условие экстремума. Для решения в этом случае используют алгоритмы, аналогичные алгоритмам градиентных методов решения непрерывно-экстремальных задач. Эти алгоритмы характеризуются временем сходимости, на порядки превышающим это время для переборных (универсальных точных) методов решения.

Для зависимости суммарной продолжительности цикла работ от порядка их выполнения на рабочих местах, по всей вероятности, не представляется возможным аналитически доказать ее дискретную выпуклость ввиду параллельности обработки партий деталей одной номенклатуры на разных рабочих местах и включения в продолжительность цикла работ разовых и регулярных профилактических ремонтов. Поэтому в предлагаемом комбинаторном методе оптимизации расписания работы рабочих мест решения, полученные в результате поиска по перестановочному многограннику подвергаются дальнейшему улучшению по алгоритму метода ветвей и границ (хотя такое улучшение может оказаться и ненужным). Процедура поиска на перестановочном многограннике повторяется несколько раз с различными отправными точками и далее наилучший из полученных вариантов используется в качестве начального решения в алгоритме метода ветвей и границ.

Для реализации перестановочного алгоритма на множестве решений задачи вводится понятие окрестности точки, в качестве которого выступает множество комбинаций перестановок, которые могут быть получены из рассматриваемой за одну транспозицию, то есть за одну перемену местами двух произвольных операций. В окрестности точки ищется перестановка с наилучшим значением целевой функции задачи, которая затем принимается в качестве следующего анализируемого варианта (следующей точки поиска). Поскольку определить число локальных минимумов задачи не представляется возможным, число реализаций поиска по перестановочному многограннику ограничивается заданным числом попыток.

Для математической реализации предложенной схемы поиска вектор решения задачи представляется в виде

(x₁ , x₂ , x₃ ,┘., x_i ,┘.., x_n)      (5)

где x_i √ соответствует номеру партии деталей, помещаемой в i-ю по номеру очередь.

Таким образом, x_i может принимать значения от 1 до n:

x_i {1,2,┘.,n}, i=1,┘,n      (6)

где n √ общее число партий деталей, запускаемых в обработку.

Допустимость решения при этом регламентируется условием

( x_i x_k , k=1,┘,n, k i ), i=1,┘n      (7)

Алгоритм поиска на перестановочном множестве включает в себя следующую последовательность действий.

1. Начальное значение вектора Х¹ выбирается как наилучшее среди полученных решений, полученных по алгоритму случайного поиска.

2. Для Х¹, отражающего очередность деталей на рабочих местах, рассчитываются времена начала запуска посредством последовательного применения выражения (2) (или (3) √ в зависимости от постановки задачи) для каждого номера очереди (i=1,┘,n) по каждому из рабочих мест (j=1,┘,m).

3. На основании полученного расписания запуска партий деталей по рабочим местам рассчитывается общая продолжительность производственного цикла по формуле (1), которая принимается в качестве значения целевой функции задачи k-го шага поиска F^k.

4. Организуется просмотр окрестности анализируемого решения как циклический перебор всех элементов вектора Х^k и просмотр для каждого из этих элементов всех возможных его перестановок с другими элементами. Для каждой из анализируемых перестановок рассчитывается свое значение целевой функции задачи по по формуле (1).

Если в процессе обзора окрестности решения Х^k удается получить значение F, лучшее, чем F^k , то происходит переход к пункту 5. алгоритма.

Если в результате просмотра окрестности точки Х^k не удается обнаружить точку со значением функции лучше, чем F^k , то F^k принимается в качестве рекордного значения целевой функции F^R , Х^k √ в качестве рекордного решения Х^R и происходит переход к пункту 6.

5. Данная точка окрестности точки Х^k принимается в качестве решения следующего шага поиска Х^k+1 , а значение F в данной точке окрестности √ в качестве значения целевой функции в (k+1)-й точке поиска - F^k+1 ; осуществляется возврат к пункту 4.

6. Если заданное число попыток реализации поиска на перестановочном множестве еще не реализовано, осуществляется переход к пункту 1., в противном случае поиск переходит в новую стадию √ применению алгоритма метода ветвей и границ √ к пункту 7.

7. Для полученного на предыдущем этапе поиска рекордного решения производится расчет оценок снизу всех соответствующих Х^R частичных решений уровней от 1 до n-1 , то есть частичных решений:

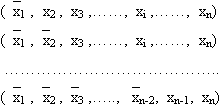    (8)

Расчет оценок снизу целевой функции задачи производится по формуле:

    (9)

где t_l^√(j,j-1)- смещение по началу обработки партии деталей номенклатуры l на (i-1)-м подающем и j-м получающем рабочих местах.

t_l^+(j,j-1)- смещение по окончанию обработки партии деталей номенклатуры l на (i-1)-м подающем и j-м получающем рабочих местах.

Такая оценка снизу несколько оптимистична, но она позволяет гарантировать, что в процессе поиска не произойдет необоснованного отсечения решений, среди которых может оказаться и оптимальное.

Применяемая далее схема метода ветвей и границ несколько специфична, ввиду специфичности множества решений перестановочной задачи, изображенного на рисунке 2, из которого видно, что число ветвлений на каждом из уровней дерева уменьшается на единицу и соответственно на предпоследнем уровне уже нет альтернативных продолжений анализируемого частичного решения (на рисунке 2 показано дерево решений для трех партий деталей).

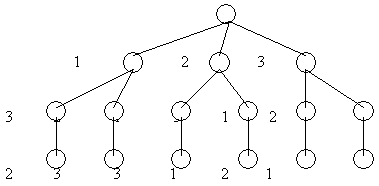
Рис. 2. Дерево решений перестановочных задач.

После получения оценок снизу для всех частичных решений, соответствующих рекордному полному решению, полученному на этапе применения перестановочного алгоритма, происходит подъем от конечной вершины дерева решений к вершине уровня n-2, то есть переход к частичному решению . Если полученная ранее оценка снизу этого уровня меньше, чем имеющийся рекорд, это частичное решение достраивается до второго производного от него полного решения. Для этого полного решения определяется значение целевой функции F, и если F< F^R, то F^R присваивается значение F, а полученное полное решение принимается в качестве нового рекордного решения Х^R.

Далее осуществляется подъем к частичному решению уровня и если полученная ранее оценка этого уровня меньше, чем имеющийся рекорд, это частичное решение достраивается до очередного частичного решения уровня , для этого частичного решения рассчитывается его оценка снизу, и так далее.

Таким образом, на каждом шаге поиска по методу ветвей и границ реализуется следующий алгоритм расчетов.

Если осуществлен просмотр всех частичных решений этого уровня и данный уровень не первый, происходит подъем к предыдущему уровню дерева решений.

Если просмотрены еще не все частичные решения этого уровня и этот уровень не (n-1)-й, выбирается следующее по счету частичное решение данного уровня и рассчитывается его оценка снизу по формуле (9). Если полученная оценка снизу меньше, имеющегося рекорда F^R , происходит спуск на следующий уровень дерева решений и формирование множества возможных частичных решений этого уровня .

Если просмотрены еще не все частичные решения этого уровня, и этот уровень (n-1)-й, выбирается следующее по счету частичное решение данного уровня, это частичное решение достраивается до производного от него полного решения, для полного решения рассчитывается значение целевой функции задачи F. Если F< F^R, то F^R присваивается значение F, а полученное полное решение принимается в качестве нового рекордного решения Х^R. Осуществляется подъем на (n-1)-й уровень дерева решений.

Если осуществлен просмотр всех частичных решений этого уровня и данный уровень первый, алгоритм поиска прекращается, в качестве оптимального решения задачи принимается решение Х^R.

Для случая, когда допускается произвольная очередность обработки партий деталей на различных рабочих местах стратегия поиска предлагаемого метода остается такой же (то есть последовательное применение перестановочного поиска из случайных точек пространства решений и метода ветвей и границ), но алгоримическая реализация несколько усложняется. Вектор решения рассматриваемой постановки задачи можно представить как объединение M векторов размерности N, каждый из которых отражает очередность запуска на j-м рабочем месте.

Х = ((x₁,x₂,..,x_n)₁,(x₁,x₂,..,x_n)₂,.., (x₁,x₂,..,x_n)_j,.., (x₁,x₂,..,x_n)_m)      (10)

Его также можно представить в виде матрицы

Перестановочный метод для задачи оптимизации запуска партий деталей в такой постановке предполагает следующий принцип определения транспозиций в перестановочном пространстве решений: в качестве транспозиции принимается перестановка любых двух компонент из одной строки матрицы Х.

При расчете целевой функции задачи в анализируемой точке окрестности текущего решения проверка ее допустимости не требуется, так как расчет времен запуска партий деталей на разных рабочих местах по выражению (2) предусматривает необходимый сдвиг начала запуска для того, чтобы обеспечить его корректность.

Также не возникает существенных сложностей и при реализации этапа поиска по методу ветвей и границ. Дерево решений этой постановки задачи выбора оптимального варианта запуска партий деталей по рабочим местам представляет объединение деревьев решений M перестановочных задач (см. рис. 2), а алгоритм получения частичных решений соответствует заполнению матрицы (11) по столбцам снизу вверх слева направо.

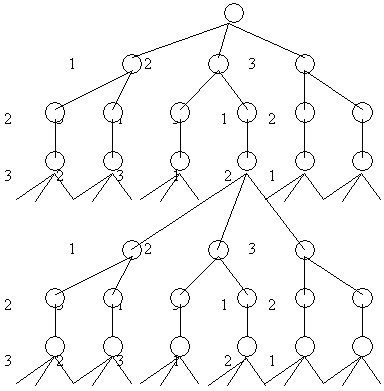
Рис. 3. Дерево решений при произвольной очередности запуска деталей на рабочих местах

Алгоритм случайного поиска остается неизменным, то есть таким же, как и при неизменной очередности обработки деталей на рабочих местах. При этом принцип неизменности очередности запуска сохранен на этой стадии поиска, что сделано для того, чтобы избежать анализа заведомо плохих решений.

Предложенный метод имеет следующие важные отличия от существующих.

Первое, в отличие от получивших распространение эвристических методов оптимизации очередности обработки партий деталей предлагаемый метод является точным и, таким образом, обеспечивает нахождение глобального оптимального решения.

Второе, метод позволяет получать глобальные решения задачи оптимизации расписания как с неизменной, так и с произвольной очередностью запуска партий деталей на различных рабочих местах.

Третье, при оптимизации очередности обработки партий деталей приведенным методом одновременно с расчетом очередности проводится построение самого расписания работ, что позволяет уменьшить время на решение этой задачи.

Четвертое, приведенный метод позволяет строить расписание работ, начиная с любой операции или рабочего места ГПЛ, не изменяя расписания работ на предыдущих операциях, что делает этот метод более гибким по сравнению с существующими. При этом появляется возможность сократить время на перерасчет расписания работ при возникновении каких-либо сбоев в производственном процессе, требующих перестройки расписания работ.

Пятое, использование пооперационной оптимизации очередности обработки партий деталей на рабочих местах, то есть с учетом расписания обработки на предыдущих рабочих местах позволяет говорить о том, что в случае перечета расписания работ внутри шага управления из-за возмущений в ходе производственного процесса новое расписание работ будет не кардинально отличаться от предыдущего. Существующие в настоящее время другие методы такой гарантии не дают, и полученные с их помощью решения могу привести к усложнению процессов производства, диспетчирования и регулирования.

Шестое, возможное число вариантов решения задачи формирования оптимального расписания при неизменной очередности запуска деталей одной номенклатуры на разных рабочих местах, как и у других перестановочных задач, равно N!, а не M^N, как это имеет место в задачах определения оптимальных выборок. Это означает, что в алгоритме метода ветвей и границ число анализируемых вариантов увеличивается не в степенной зависимости от размерности задачи.

Седьмое, при решении задачи формирования оптимального расписания при произвольной очередности запуска деталей одной номенклатуры на разных рабочих местах множество вариантов решения возрастает в степенной зависимости от M, и определяется величиной

К= (N!)^м

где N - количество обрабатываемых партий деталей;

М - количество рабочих мест (операций технологического маршрута).

Однако при этом возрастает эффективность отсечений по оценкам снизу частичных решений, так как в анализируемые подмножества входят заведомо плохие варианты запуска. Таким образом, увеличение размерности задачи в M раз вовсе не означает увеличение времени счета в этой же пропорции.

СПИСОК ЛИТЕРАТУРЫ

1. Парамонов Ф.И. Моделирование процессов производства. - М.: Машиностроение, 1984.-231 с.

2. Рейнгольд Э., Нивергелы Ю., Део Н. Комбинаторные алгоритмы √ теория и практика. / Пер. с англ. Под ред. Алексеева. √ М.: Мир,1980.-478 с.