3 of 7

3. Брадобрей не бреется

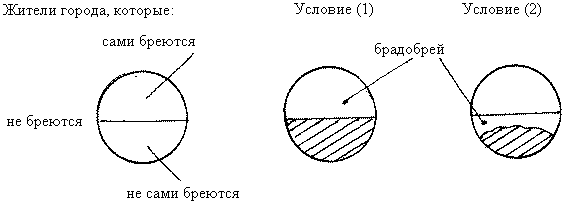
Знаменитый парадокс брадобрея придуман Б. Расселом для иллюстрации другого парадокса. Этот другой парадокс возникает, по его мнению, когда "некие математические конструкции приводят к множествам, которые включают себя в качестве одного из своих членов." ([2] , c. 23).

Мы разберем сейчас парадокс брадобрея, но вначале обратим внимание на поучительное утверждение: "Нельзя съесть торт так, чтобы он остался цел". В этом утверждении нет никакого парадокса! Торт, который одновременно съеден и не съеден, просто не существует.

Займемся парадоксом брадобрея.

"Брадобрей бреет всех тех (1) и только тех (2) жителей города, которые не бреются сами. Кто бреет брадобрея?" ([2] , c. 22). Парадокс брадобрея заключается в том, что, якобы, нельзя ответить на этот вопрос.

Чтобы понять ситуацию, разобьем жителей города на три группы. Это разбиение показано на левом рисунке: те, кто бреется самостоятельно, - сверху; те, кого бреют, - снизу; кто вообще не бреется (монахи, дети, женщины...) - вне эллипса.

Рассмотрим сначала действие условия (1). Пусть брадобрей бреет всех тех, которые не сами бреются, то есть всю нижнюю половину эллипса (штриховка отмечает клиентов брадобрея). Но условие (1) разрешает ему брить и того, кто сам бреется, то есть самого себя. Условие (1) разрешает ему расположиться в верхней половине эллипса, где жители сами бреются, и брить себя там. Это показано на среднем рисунке.

Если же действует условие (2), и брадобрей бреет только тех, которые не сами бреются, это означает, что он бреет часть нижней половины эллипса и не бреет себя, то есть не находится в верхней половине эллипса. Но жители из нижней половины могут быть побриты не брадобреем, а кем-то еще. И брадобрей может находиться среди этих людей (правый рисунок). Так что брадобрея может брить его приятель, а брадобрей будет брить заштрихованную часть нижней половины эллипса.

Но если действуют оба условия, (1) и (2), то брадобрею нет места в эллипсе. Он, значит, не бреется вообще. И тут нет никакого парадокса. Он, сталь быть, либо монах, либо робот, либо ребенок, либо не житель города... А если в городе нет никого, кроме бреющихся мужчин, и, стало быть, внешность эллипса пуста, то брадобрей, удовлетворяющий условиям (1) и (11), попросту не существует, как торт, который был съеден, но остался цел. Нелепо спрашивать в этом случае, кто его бреет. Множество таких брадобреев, как и множество таких тортов - пусто.

И тут мы заметим, что заданный вопрос, "Кто бреет брадобрея?", был некорректен с самого начала так же, как классический вопрос: "Зачем ты бьешь своего отца?" Прежде, чем спрашивать, кто бреет брадобрея, надо получить согласие, что его кто-то бреет.