УДК: 510.27

Р.И.Храпко

Серьезное отношение к логическим парадоксам, типа парадоксов Зенона, Бертрана Рассела, свидетельствует о слабоумии представителей вида Homo Sapiens. Автор намерен обратить внимание на несостоятельность распространенных логических парадоксов и тем отвести попытки дискредитировать логику.

1. Люди и логика

Люди не любят логику. Она мешает обманывать себя и других и выдавать желаемое за действительное. Возможно, поэтому замечательный драматург Эжен Ионеско издевался над логикой: некто Логик, персонаж его пьесы "Носорог", говорит Старому господину: "А вот вам еще силлогизм. Все кошки смертны. Сократ смертен. Следовательно, Сократ - кошка."

Весьма популярен Гегель, который стремился опровергнуть логический закон исключенного третьего ([1] , с.64):

"Положение об исключенном третьем утверждает, что нет ничего такого, что не было бы ни А, ни не-А, что нет такого третьего, которое было бы безразлично к этой противоположности. В действительности же имеется в самом этом положении третье, которое безразлично к этой противоположности, а именно само А..."

В.И. Ленину импонировало такое стремление. "Это остроумно и верно", отметил он в своих ⌠Философских тетрадях■. Не случайно, видимо, у Владимира Ульянова при блестящей успеваемости была тройка по логике.

Логику не любят верящие в парапсихологию, НЛО и прочее. Они хотели бы опереться на такое рассуждение: "В прошлом люди не подозревали о существовании бактерий, о возможностях радио. А теперь - это реальность! Так же и паранормальные явления, которые сейчас вызывают сомнения, будут признаны реальностью в будущем".

Но логика не дает основания для такого вывода! Наоборот, многочисленные ошибки людей в прошлом увеличивают вероятность ошибок в настоящем. Логика исключает мистику. Такие понятия как "светящаяся темнота" или принцип единства части и целого - алогичны. Естественно, логику не любят верующие. "Верую, потому что нелепо" - сказал богослов 2 - 3 века Тертуллиан о судьбе Христа.

Сильнее всего дискредитируют логику логические парадоксы. Возможно, поэтому их придумано много со времен Древней Греции. Эта заметка посвящена разрешению парадоксов. Открытым остается вопрос, почему такую возможность не замечают многие великие умы.

В парадоксе Зенона "Ахиллес" утверждается, что быстроногий Ахиллес не сможет догнать черепаху, которая в момент старта находится на некотором расстоянии от него. Ход рассуждения тут таков. Прежде, чем догнать черепаху, Ахиллес должен достичь места, где она находилась вначале. Но за это время черепаха, конечно, немного удалится от Ахилесса. Далее герой снова будет вынужден пробежать разделяющее их расстояние, но черепаха снова хоть немного, но уползет вперед. И Ахиллес, занятый этим бесконечным процессом, никогда не сможет его завершить и поэтому не сможет догнать черепаху.

Более того, даже если черепаха, услышав сигнал к старту, не сдвинется со своего места, Ахиллес, все равно, не достигнет ее, так как ему нужно будет пройти сначала половину разделяющего их промежутка, но прежде - половину его половины и так далее до бесконечности. В этом заключается второй парадокс Зенона, известный под названием "Дихотомия", из которого делается вывод, что Ахиллес вообще не сможет сдвинуться с места и движение вообще невозможно. Ибо, чтобы пройти даже как угодно маленький отрезок, требуется бесконечная последовательность действий.

Обсуждению парадоксов Зенона посвящена обширная литература, в том числе и современная. В частности, как это ни странно, по мнению Бертрана Рассела, решение парадоксов Зенона требует теории типа канторовской теории множеств ([2] с.187).

На наш взгляд, мнение Рассела является сильным преувеличением. Совсем нетрудо принять, что при суммировании бесконечного количества слагаемых может получиться конечное число, если величина слагаемых быстро убывает: 1/2 + 1/4 + 1/8 + 1/16 + ... = 1. Поэтому бесконечная последовательность действий может быть выполнена за короткое время, если длительность каждого последующего действия быстро убывает, и Ахиллес, конечно, быстро догонит черепаху, потому что при постоянной скорости его движения члены ряда 1/2, 1/4, 1/8, 1/16,,... представляют не только отрезки пути, но и отрезки времени.

Зенон, конечно, понимал, что если стрела летит из пункта A в пункт B со скоростью v, а расстояние между A и B равно S, то время полета будет t = S/v. Надеемся, Зенон понимал, что если отрезок S разделить пополам, а потом половину еще пополам и т.д., то от этого длина отрезка S не увеличится. Но, видимо, абстрактное мышление в Древней Греции не было развито достаточно для того, чтобы перенести это рассуждение на отрезок времени, t. Зенон считал, что если отрезок t разделить пополам, а потом половину еще пополам и т.д., то от этого деления длина отрезка t увеличится до бесконечности.

Да и теперь такое заблуждение весьма распространено. Мы приведем для иллюстрации типичное ошибочное рассуждение [3] :

"Ясно, что сумма ряда 1/2 + 1/4 + 1/8 + 1/16 + ... равна единице, но в точности единице она равна только потенциально, а актуально, в каждый конкретный момент времени, она всегда будет хоть чуть-чуть меньше единицы. В точности равной единице она может стать только в бесконечно удаленном будущем, то есть никогда. Значит, Ахиллес никогда не сможет догнать черепаху?"

Как ни удивительно, но для "разрешения" парадоксов Зенона привлекают квантовую механику. Авторы работы [4] , как и автор работы [3] , считают рассуждение Зенона верным, а выход из парадоксов видят в следующем обстоятельстве. Замораживание всех процессов, которое должно было бы произойти, согласно рассуждениям Зенона, не происходит в силу того, что бесконечная делимость времени, используемая Зеноном, невозможна из-за квантовомеханического соотношения неопределенностей энергии и времени, E t > h, поскольку уменьшение времени на измерение местоположения объекта, требует увеличения затрачиваемой на него энергии.

В качестве примера здравых оценок парадоксов Зенона приведем высказывание известного французского математика Поля Леви (P. L'evy). В 1959 году он писал:

"Как можно воображать себе, что время остановится из-за того, что некий философ занимается перечислением членов бесконечного ряда. Признаюсь, я никогда не понимал, как люди, в других отношениях весьма разумные, могут оказаться смущенными подобными парадоксами. Мой теперешний ответ есть тот самый, который я дал, когда мне было 11 лет, старшему, рассказавшему мне этот парадокс. Я резюмировал тогда такой немногословной формулой: "Этот грек был идиотом". Я знаю теперь, что нужно выражать свои мысли в более вежливой форме и что, возможно, Зенон излагал свои парадоксы только для того, чтобы проверить разумность своих учеников. Но мое удивление перед умами, смущаемыми сходящимся рядом, осталось тем же."

Заметим, что Гегель высоко отзывался о Зеноне: "Особенность Зенона - диалектика... Он - зачинатель диалектики... У Зенона мы находим истинно объективную диалектику".

Знаменитый парадокс брадобрея придуман Б. Расселом для иллюстрации другого парадокса. Этот другой парадокс возникает, по его мнению, когда "некие математические конструкции приводят к множествам, которые включают себя в качестве одного из своих членов." ([2] , c. 23).

Мы разберем сейчас парадокс брадобрея, но вначале обратим внимание на поучительное утверждение: "Нельзя съесть торт так, чтобы он остался цел". В этом утверждении нет никакого парадокса! Торт, который одновременно съеден и не съеден, просто не существует.

Займемся парадоксом брадобрея.

"Брадобрей бреет всех тех (1) и только тех (2) жителей города, которые не бреются сами. Кто бреет брадобрея?" ([2] , c. 22). Парадокс брадобрея заключается в том, что, якобы, нельзя ответить на этот вопрос.

Чтобы понять ситуацию, разобьем жителей города на три группы. Это разбиение показано на левом рисунке: те, кто бреется самостоятельно, - сверху; те, кого бреют, - снизу; кто вообще не бреется (монахи, дети, женщины...) - вне эллипса.

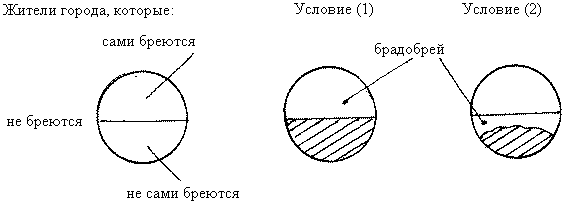
Рассмотрим сначала действие условия (1). Пусть брадобрей бреет всех тех, которые не сами бреются, то есть всю нижнюю половину эллипса (штриховка отмечает клиентов брадобрея). Но условие (1) разрешает ему брить и того, кто сам бреется, то есть самого себя. Условие (1) разрешает ему расположиться в верхней половине эллипса, где жители сами бреются, и брить себя там. Это показано на среднем рисунке.

Если же действует условие (2), и брадобрей бреет только тех, которые не сами бреются, это означает, что он бреет часть нижней половины эллипса и не бреет себя, то есть не находится в верхней половине эллипса. Но жители из нижней половины могут быть побриты не брадобреем, а кем-то еще. И брадобрей может находиться среди этих людей (правый рисунок). Так что брадобрея может брить его приятель, а брадобрей будет брить заштрихованную часть нижней половины эллипса.

Но если действуют оба условия, (1) и (2), то брадобрею нет места в эллипсе. Он, значит, не бреется вообще. И тут нет никакого парадокса. Он, сталь быть, либо монах, либо робот, либо ребенок, либо не житель города... А если в городе нет никого, кроме бреющихся мужчин, и, стало быть, внешность эллипса пуста, то брадобрей, удовлетворяющий условиям (1) и (11), попросту не существует, как торт, который был съеден, но остался цел. Нелепо спрашивать в этом случае, кто его бреет. Множество таких брадобреев, как и множество таких тортов - пусто.

И тут мы заметим, что заданный вопрос, "Кто бреет брадобрея?", был некорректен с самого начала так же, как классический вопрос: "Зачем ты бьешь своего отца?" Прежде, чем спрашивать, кто бреет брадобрея, надо получить согласие, что его кто-то бреет.

Обнаружив, что "парадокс брадобрея" не имеет отношения к упомянутой проблеме теории множеств, займемся напрямую этой проблемой.

Итак, пусть рассматриваемое множество состоит из всех множеств. То есть членами рассматриваемого множества являются все множества. Содержит ли оно себя в качестве одного из своих членов?

Наш ответ будет отрицательным: множество всех множеств не содержит себя. Для доказательства мы просто построим множество всех множеств, основанное на двух элементах: a и b. Назовем эти элементы множествами первого порядка и, чтобы показать это, заключим их в скобки: (a), (b). Каждое из этих множеств содержит по одному члену. А множество множеств первого порядка содержит два члена.

Теперь рассмотрим множество множеств первого порядка как элемент множества второго порядка ((a)(b)). Множество второго порядка состоит из одного члена. Присоединим его к множествам (a) и (b). Получим множество, состоящее из трех членов: (a), (b), ((a)(b)).

Рассматривая различные множества, составленные из этих членов, ((a)((a)(b))), ((a)(b)((a)(b))), ((b)((a)(b))), получим множество третьего порядка, состоящее уже из трех членов. Присоединим его к ранее построенным множествам.

Продолжая этот процесс до бесконечности, мы построим множество всех множеств, основанное на двух элементах. Любой член этого множества будет являться множеством, состоящим лишь из членов, конкретного порядка, определяемого числом скобок. Ни один член этого множества не будет являться самим этим множеством, хотя, по построению, это множество будет содержать любое множество, основанное на a и b.

Попытка включить в рассматриваемое множество вопреки нашей процедуре само рассматриваемое множество в качестве своей части обречена на неудачу. Это доказывает история несчастного попа, у которого была собака, а он ее убил и надпись написал, что у попа была собака, а он ее убил и надпись написал, что... Неудача с надписью произошла именно потому, что поп пытался в надпись, которая является частью истории, засунуть всю историю, включая саму надпись. Целое не может войти составной частью в свою часть, целое всегда больше части. Для того, чтобы целое было заключено в часть этого целого, процедура попа должна быть завершена, а это невозможно, потому что процедура бесконечна и однородна в том смысле, что последующие этапы не отличаются друг от друга.

В отличие от процедуры попа, нашу процедуру создания множества всех множеств не надо завершать, как не надо завершать процесс создания натурального ряда чисел по рекуррентной формуле x_n = x_n-1 + 1 для того, чтобы констатировать существование натурального ряда.

Процедура включения целого в качестве части обречена на неудачу, потому что затягивается до бесконечности. Это хорошо видно на обложке журнала, представленной здесь.

Можно, однако, получить кажущееся решение проблемы включения целого в свою часть, использовав обозначение "это". Именно, историю попа можно быстренько рассказать так: "У попа была собака, он ее убил и об этом написал".

Как раз такой жульнический прием использует Шалтай-Болтай по отношению к Алисе в парадоксе, приведенном в книге [5] .

Шалтай-Болтай спросил Алису:

- Можно ли считать "нет" правильным ответом на этот вопрос?

- На какой вопрос? - спросила Алиса.

- На вопрос, который я только что задал, - пояснил Шалтай-Болтай. Алисе следовало бы вежливо попросить Шалтая-Болтая: "А не могли бы Вы, любезный, задать мне вопрос в явном виде, без слов типа "этот вопрос"? И тогда Шалтаю-Болтаю пришлось бы продираться сквозь бесконечность:

- Можно ли считать "нет" правильным ответом на вопрос: "Можно ли считать "нет" правильным ответом на вопрос: "Можно ли считать ...

А Алиса могла бы тем временем подкармливать его тортом, который съеден.

"По преданию, Эпименид утверждал, что все критяне лжецы. Верно ли это утверждение, если учесть, что сам Эпименид родом с острова Крит?" - так выглядит парадокс лжеца ([2] c. 9). Однако, если освободить его от словесных нагромождений, парадокс сводится к вопросу: истинно или ложно простое высказывание "Я лгу"? [6] .

И вот в этой простоте становится ясно, что высказывание "Я лгу", которое нам предстоит оценить, не закончено, а потому - непонятно. Прежде, чем его оценивать, следует уточнить, что именно "лжец" лжет. Возможно, "лжец" скажет, что он "лжет, что он лжет". Но тогда следует спросить, что именно он лжет, что он лжет.

Становится ясно, что наш "лжец" еще менее честен, чем Шалтай-Болтай. Тот хоть произнес слова "этот вопрос". "Лжец" же не говорит: "Я лгу это". Он просто умолкает на полуслове, чтобы ввести нас в недоумение. На самом деле, он должен произнести следующее: "Я лгу, что я лгу, что я лгу, что ..." И когда он закончит свое высказывание, тогда мы ответим, истинно оно или ложно.

Когда некто говорит: "Я лгу, что купил эту книгу", он говорит правду или лжет. Это зависит от того, откуда у него эта книга. Если ему ее подарили, его слова - правда. Если он купил ее, его слова - ложь. Когда некто просто говорит "Я лгу", он в действительности не высказывает никакого утверждения, ни правдивого, ни ложного.

Мы закончим разрешение парадоксов решением давнего спора, что было сначала, курица или яйцо? Очевидно, что сначала было яйцо, потому что птицы произошли от ящеров, которые размножались, как и птицы, при помощи яиц. В процессе эволюции менялось содержимое яиц. И однажды из яйца вылупилось создание, которое, по нашему мнению, мы уже можем назвать не ящером, а птицей.

Вот если бы курицы прежде были живородящими, и однажды, вместо цыпленка, некая курица произвела бы яйцо, из которого бы вылупилась яйценосная курица, тогда вначале была бы та некая курица.

Сокращенный вариант этой статьи был опубликован в журнале "Химия и жизнь" [7] . Настоящая статья была отклонена без объяснений следующими журналами: "Вопросы философии", "Наука и жизнь", "Знание - сила", "Квант".

Список литературы

1. Гегель Г.В. Наука логики. Т.2. - М.: ИПЛ, 1970.- 545 с.

2. Гарднер М. А ну-ка догадайся. - М.: Мир, 1984.- 212 с.

3. Жвирблис В.Е. Так ли глуп был этот грек? // Химия и жизнь. - 1998, N4.- с.76-77.

4. Kofman A.G., Kurizki G. Acceleration of quantum decay processes by frequent observations. // Nature. - 2000, vol 405.- p.546-549.

5. Смаллиан Р. Как же называется эта книга? - М.: Мир, 1981.- 291 с.

6. Философский энциклопедический словарь. - М.: Советская энциклопедия, 1983.- 840 с.

7. Храпко Р.И. Люди и логика. // Химия и жизнь. - 1998, N4.- с.76-77.