УДК 621.81(31)

Н. П Mясников., Г. Л. Родионов, А. C. Сидоренко

Представлены анализ и обобщение расчетных и экспериментальных исследований локального напряженно-деформированного состояния и прочности пластин и оболочек с несквозными повреждениями, имеющими различную геометрию. Показано, что наиболее эффективным путем расчетного определения локальных напряжений и деформаций в зоне несквозного повреждения с входящим углом является использование МКЭ и определенной технологии КЭ моделирования. На основе объемных КЭ большой размерности разработаны численные модели пластин с несквозными отверстиями различного вида. Эти модели позволяют оценивать максимальную величину напряжений и локального прогиба, влияние зачистки повреждения на величину концентрации напряжений и, следовательно, уменьшить опасность повреждения.

1. Введение

В процессе эксплуатации ЛА возникают повреждения конструкции, приводящие к снижению исходных уровней прочности и долговечности. Характерными эксплуатационными повреждениями обшивки и силовых элементов являются отверстия, трещины, коррозия, вмятины, царапины, надиры. Здесь рассматриваются несквозные повреждения, к которым относятся царапины, надиры, коррозионные пятна, поверхностные трещины. Они могут быть локальными, например, в виде сферической лунки или протяженными в одном направлении и иметь входящие углы, являющиеся источниками концентрации напряжений (КН). Несквозные повреждения в ряде случаев могут быть более опасными с точки зрения образования и развития трещин, чем сквозные /1/. Определение зависимостей параметров НДС конструкции от вида, размеров и формы повреждений в сечении и в плане позволяет оценить предельные значения параметров повреждения для заданных условий нагружения.

Перечисленные выше несквозные повреждения могут быть представлены в виде местных утонений или несквозных отверстий (НО) различной формы в элементах конструкций, которые вызывают КН в зонах резкого изменения сечения и больших кривизн поверхности. Практически единственным способом уменьшения КН является местная плавная зачистка НО, уменьшение кривизны на стыке поверхностей.

Далее представлены расчетные и экспериментальные зависимости для оценки параметров НДС и местной прочности тонкостенных конструкций типа пластин и цилиндрических оболочек в зоне несквозных повреждений. В настоящее время отсутствуют обоснованные методы оценки локального НДС и предельных нагрузок для элементов тонкостенных конструкций, имеющих местные утонения, с учетом пластических деформаций. Наиболее реальным путем получения оценок является использование полуэмпирических соотношений.

2. Оценка характеристик локального НДС конструкции в зоне НО

Расчетная модель тонкостенной конструкции обычно принимается в виде круглой или прямоугольной пластины с центральным углублением, нагруженной усилиями растяжения p, действующими в плоскости (рис. 1.), а характеристики НДС определяются из решения трехмерной или осесимметричной задач теории упругости. Зона повреждения ограничивается круговым контуром, и далее рассматривается круговое НО. Растяжение предполагается простым или осесимметричным (для круглой пластинки), что позволяет свести задачу к двумерной. Это решение дает оценку величины КН (K= /p) и позволяет определить уровень разрушающих или предельных нагрузок.

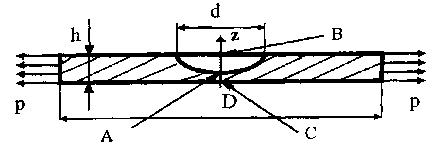
Рис. 1

Если размер повреждения в плане существенно больше толщины оболочечной конструкции, то может потребоваться учет кривизны оболочки и, следовательно, НО уже не будет ограничено поверхностями вращения. Поэтому в случае утонений имеющих размеры в плане, существенно превышающие номинальную толщину стенок, элементы конструкций моделируются в виде круглой пластинки или пологой панели, нагруженных мембранными усилиями и поперечным давлением.

В большинстве известных работ рассматривается пластина постоянной толщины, имеющая в центре НО в виде сферической, эллиптической или скругленной цилиндрической лунки.

2.1 Аналитические и расчетно-экспериментальные оценки

Задача о двустороннем растяжении бесконечной пластины единичной толщины c полусферической лункой решена полуобратным методом /2/.

Компоненты напряжения представляются в виде рядов, члены которых имеют сомножители, определяемые из бесконечной системы линейных алгебраических уравнений. Коэффициенты системы выражены через табличные несобственные интегралы. Для компонент нормального напряжения _x, _y выполняется условие (_x)_r = ( _y)_r = p, в котором p - равномерное по толщине растягивающее напряжение.

НДС для полосы, растянутой в направлении длины L исследовано расчетно- экспериментальным методом /3/. Определено влияние ширины полосы b на коэффициент КН в зоне НО, имеющем вид шарового сегмента с диаметром основания d. На основе экспериментальных данных одна группа компонентов тензора напряжений представлена квадратичными приближениями по толщине. Компоненты другой группы считаются пренебрежимо малыми. Вводится функция напряжений:

(x, y, z) = - 0.5 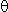₀ z²/ (1+ ) + ₁ z + ₀ ,

в которой функция ₀ зависит от ₀ , а функции ₀ , ₁ имеют вид:

(x, y) = (x² -1)⁴ (y² - L²)⁴ a_mn cos (n - 0.5) x cos (m - 0.5) y.

Задача содержит 2N² неизвестных, которые определяются из условия минимума потенциальной энергии упругой деформации. Коэффициент КН (ККН) при всестороннем растяжении получен путем суммирования напряжений при одноосных растяжениях и сопоставлен с аналогичным значением из / 2 /, которое считается точным.

Изменение напряжения _y вдоль оси z по толщине пластины вдоль оси, проходящей через центр полусферического углубления, показано на рис. 2. Кривые соответствуют расчетным и экспериментальным данным для одноосного и двухосного растяжения.

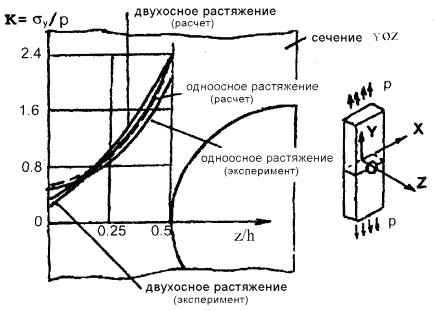
Рис. 2

Для сферических углублений наиболее опасными точками являются центр сферической поверхности (т. А) и точки контура сферического углубления, расположенные под углом /2 к направлению максимальных напряжений (т. В) (рис. 1). На рис. 3 показаны расчетные зависимости ККН от параметра в точке А, полученные для одноосного (1) и двухосного растяжения напряжениями "p". Соответствующие экспериментальные данные для = 0.5 отмечены как графики 3 и 5 /3/. Из сопоставления экспериментальных и расчетных зависимостей К() в характерных точках А, В и С в зоне сферического НО видно, что вследствие влияния изгиба, характер изменения напряжений в точках А и С, расположенных на оси z, существенно различается (рис. 4). Различие между напряжениями для случаев одноосного и двухосного растяжения относительно небольшое, причем для экспериментальных данных это различие меньше, чем для расчетных. В точке А большему значению ККН соответствует двухосное растяжение. В точках В и С напряжения при одноосном растяжении оказываются больше, чем при двухосном. Изменение относительного размера d/b в пределах 0.2 - 0.45 мало влияет на величину K=_y/ p. Расчетные значения К для одноосного растяжения получаются выше экспериментальных (рис. 2- 4).

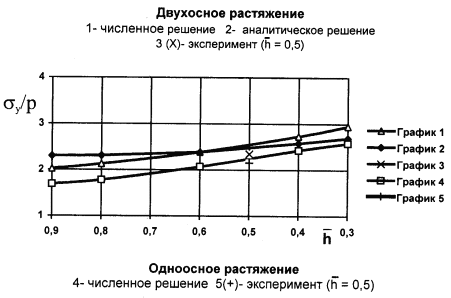
Рис. 3

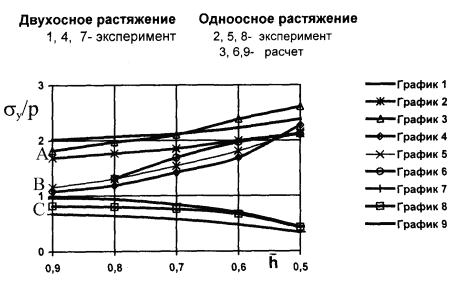
Рис. 4

В работе /4/ полуэмпирическим методом определены предельные значения внутреннего давления или размеров НО для цилиндрических оболочек. Использовались результаты испытаний на внутреннее гидростатическое давление до разрушения оболочек из сплавов СП-43, Эл- 65, Эл- 257, на поверхности которых были нанесены углубления. Отношение толщины оболочек к диаметру находилось в интервале 0.01365- 0. 00118.

Дно углубления рассматривалось как жестко- пластическая круглая шарнирно опертая пластинка с толщиной h₁ и диаметром d₁, для которой предельное значения давления составляет q_пред = 6 _т h₁²/ d₁² ( _т - ордината диаграммы жесткопластического деформирования при > 0). Эта формула использована с учетом того, что в экспериментах разрушение утоненного участка начиналось в его центре. Кроме поперечного давления в плоскости пластины действует кольцевое растягивающее напряжение _к = 0.75 ₁ ( ₁ - кольцевое напряжение в цилиндрической оболочке). Действие растяжения уменьшает величину предельного давления до величины q_пред =2.64 _т h₁²/ d₁².

Далее принималось, что _т = _в (_в - наибольшая ордината диаграммы растяжения жестко- пластического материала) и что утоненный участок не влияет на предельное давление для оболочки в целом р_р, т. е. выполняется условие q_пред р_р. Из этого условия и геометрических соотношений с учетом радиуса зачистки получена формула для допустимого диаметра утонения (по границе его зачистки в плане):

d h^0.5 (1.15 D^0.5 + 14.14 (1 - )^0.5) мм;      = h₁/ h.      (1)

Эта формула применима для тонких оболочек (D/ h 50) из высокопрочных сталей с отношением d/ h 10 (D/ d 5-6) и радиусом зачистки 25 мм (обычным в практике). При меньших значениях D/ d оценки величины q_пред будут заниженными.

Эксперимент по оценке разрушающего давления показал, что оболочки из высокопрочных сталей сохраняют несущую способность при размерах утоненных участков на 10 - 20 % превышающих значения, определяемые по данной формуле. Это обусловлено принятым условием шарнирного закрепления. Для жесткого закрепления краев пластины расчетная оценка величины d будет на 20 - 25 % выше, чем для шарнирного. Эта формула применима также для удлиненных НО, если наибольший размер принимается за d, а другой - не превышает d/2. Экспериментальные данные по значениям отношения q_пред/p_р для цилиндрических оболочек, приведенные в таблице, показывают, что здесь местные утонения оказывают заметное влияние на несущую способность оболочек при значениях < 0.60.7, т.е. формула (1) применима для НО, имеющих глубину > 0.3h.

Проведенный анализ показал, что основными факторами, определяющими изменение величины ККН, являются относительные величины и = d/(h-h₁). Аналитическое и экспериментально- теоретическое определение характеристик локального НДС в зоне НО весьма сложны в вычислительном плане. В основном для решения подобных задач используется метод конечных элементов (МКЭ).

2.2 Оценки НДС на основе применения МКЭ

Сферическое и полуэллипсоидальное НО

В большинстве работ характеристики НДС определяются для расчетной модели элемента тонкостенной конструкции c НО, представленной на рис. 1.

НДС круглой, равномерно растянутой стальной пластины с НО в виде полусферы, шарового сегмента или полуэллипсоида, имеющей радиус R и отношения R/h 5.25, R/r 2.5 (r- радиус НО) исследовано в работе /5/. Для оценки параметров НДС используется программа решения осесимметричных задач теории упругости.

Зависимости ККН - К_m, К_r, К соответственно для меридиональных, радиальных и тангенциальных напряжений от параметра близки к линейным и описываются регрессионными соотношениями, полученными путем обработки результатов численного эксперимента:

К_m1 = К_r1 =К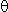₁ = 2.53 - 0.145- 0.13 + 0.195 (1-) + 0.004²,

К_m2 = К_r2 =К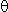₂ = 2.7 - 0.18 - 0.22 + 0.19 (1 - ) + 0.0055².       (2)

Здесь индексами "1" и "2" обозначены ККН для сферического и полуэллипсоидального НО соответственно.

Характер зависимости коэффициентов концентрации меридиональных напряжений К_m1,2 в центре углублений от параметра представлен на рис. 5. Штриховые линии соответствуют зависимостям для К_m1, сплошные- для К_m2. Данные по ККН для полусферической лунки /5/ отличаются от аналогичных данных работы /2/ в третьем знаке.

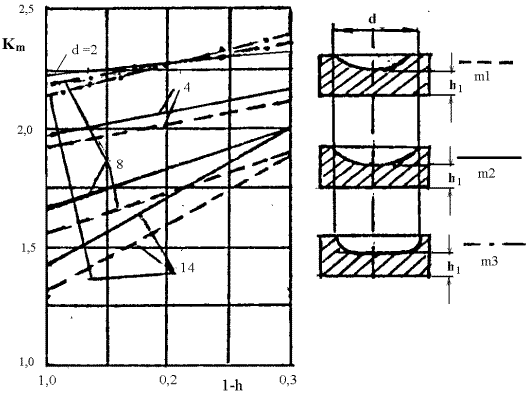
Рис. 5

Зависимости (2) применимы, вообще говоря, для значений параметров 4 1, 0.9 0.7 и показывают, что КН увеличивается с ростом глубины повреждения и уменьшением его протяженности в плане.

Решение упругой и упругопластической задач для полосы со сферической лункой при действии на торцах растягивающих напряжений p получено с использованием МКЭ и метода переменных параметров упругости /6/. Расчетные зависимости ККН от величины растягивающего напряжения для двусторонней лунки лежат выше соответствующих экспериментальных значений (рис 6). Эпюры ККН при постоянном значении p=16.5 МПа (рис. 7, 8) показывают, что при уменьшении параметра величина ККН возрастает, а его возрастание приводит к переходу материала в пластическое состояние при меньшей внешней нагрузке. Так как здесь КЭ модель (КЭМ) описывает плоское напряженное состояние и КЭ моделирование по толщине может быть весьма грубым, то представленные результаты следует рассматривать как качественные.

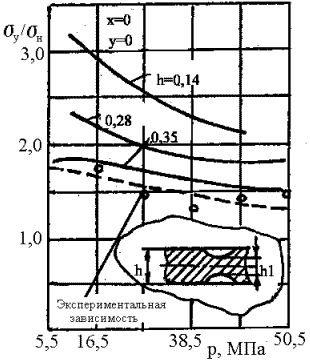
Рис. 6

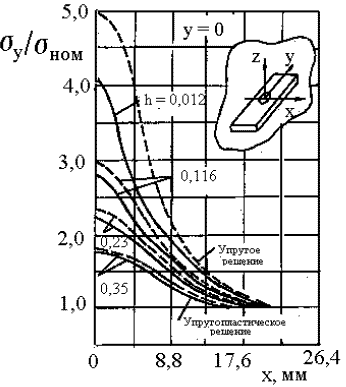
Рис. 7

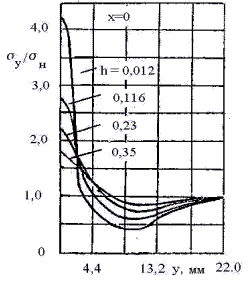
Рис. 8

Цилиндрическое НО

Соотношения (2) для ККН в радиальном, меридиональном и тангенциальном направлениях в зоне НО при осесимметричном растяжении получены для круглой пластинки со сферическим (индекс 1) или полуэллипсоидальным (индекс 2) НО. Для цилиндрического НО в такой же пластинке (индекс 3) подобные соотношения имеют вид /5/:

К_m3 = 2.58 - 0.39 - 0.01 + 0.06 (1-);

К_r3 = 2.56 - 0.022 - 0.4 + 0.06 (1-);

К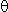₃ = 2.59 - 0.13- 0.2 + 0.135 (1 - )+ 0.0045².       (3)

Они справедливы для кругового цилиндрического НО, имеющего скругление входящего угла с радиусом равным глубине h-h₁. Зависимости для коэффициентов концентрации меридиональных напряжений К_m3 в центре такого НО показаны на рис. 5 штрихпунктирными линиями.

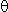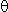
Если цилиндрическое НО не имеет скругления входящего угла, то максимальная КН возникает не в центральной части повреждения, а на его контуре. Характер изменения максимальных значений величины К = 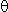/ p для прямоугольной пластинки с таким НО при одноосном растяжении напряжением p представлен на рис. 9, 10 /7/. Проиллюстрировано влияние относительной глубины НО (параметра 1-) для точки внутреннего контура с координатой 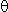= / 2 при различных относительных размерах d/ h (рис.9) и изменение К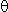 по толщине пластинки при 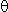= / 2 и различных значениях величины (рис. 10). При увеличении глубины НО величина К растет и в предельном случае, для сквозного отверстия, среднее по толщине значение К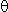 = 3, что соответствует решению задачи Кирша. Моделирование НО здесь выполнено с помощью объемных восьмиузловых КЭ. Через 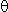обозначен угол между направлениями давления на грани трехмерной КЭМ p и плоскостью сечения. Координата z отсчитывается по нормали от поверхности пластинки.

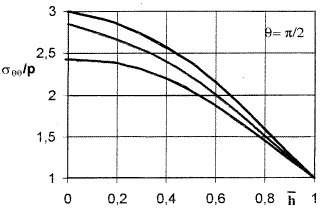
Рис. 9

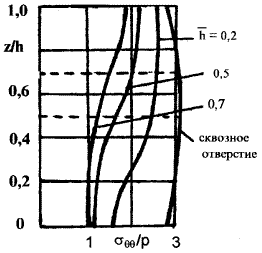
Рис. 10

Особенностью НДС для НО без скругления входящего угла является значительный уровень касательных напряжений _rz в зоне, прилегающей к внутреннему контуру НО. Распределение напряжений _rz по толщине в сечении 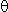= 0 для отверстий различной глубины показано на рис. 11. Напряжения _rz изменяются в направлении оси z по параболическому закону, резко возрастают вблизи внутреннего контура НО и достигают максимального значения 0.73p на расстоянии 0.02d от контура НО (при = 0.5) /7/.

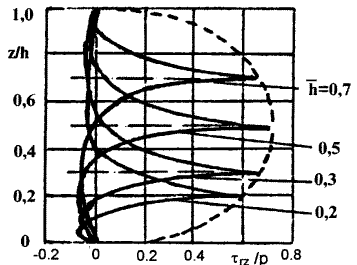
Рис. 11

Пластина с односторонним НО при растяжении изгибается. Прогиб направлен в сторону НО, а величина его определяется, в основном, относительной глубиной 1-. При уменьшении увеличивается прогиб дна НО, а общий размер зоны изгиба незначительно превышает размер d. При уменьшении глубины НО размер зоны изгиба пластины увеличивается и может превышать 2.5 d.

Исследование НДС цилиндрических оболочек с НО с помощью МКЭ сводится к моделированию сегмента в окрестности НО /8-10/. Используются двадцатиузловые объемные КЭ /8/ или КЭ, специально предназначенные для расчета НДС многослойных оболочек и оболочек, ослабленных НО /9, 10/. Для упрощения решения рассматриваются двусторонние НО, симметричные относительно срединной поверхности, что исключает изгибно- растягивающие компоненты НДС, свойственные поверхностному НО. При этом сегмент оболочки представляется в виде пластины, которая условно разделяется на три слоя. В работе /8/ моделируется половина цилиндрической оболочки с использованием объемных и двумерных КЭ. Мембранные напряжения здесь определяются только на двумерных элементах расположенных на внутренней и внешней поверхностях оболочки и на ее торцах. КЭМ протестирована путем расчета оболочки без НО.

Проведенный анализ показал, что определение ККН из решения упругой задачи с помощью библиотеки традиционных элементов является малоэффективным из-за относительно больших затрат ресурсов для получения требуемой точности оценок. Известные расчетные оценки КН для цилиндрического НО без скругления входящего угла имеют существенный разброс и непригодны для практического использования. Могут быть использованы экспериментальные данные и оценки для НО с регулярным профилем. Получаемые результаты следует сопоставлять со справочными данными для известных моделей КН. Для решения подобных задач необходимо использовать объемные КЭ большой размерности или специализированные КЭ, которые позволяют моделировать пластины и оболочки, ослабленные НО произвольной формы в плане.

2.3 Экспериментальные исследования НДС в зоне НО

Экспериментальные исследования локального проведены на пластинах из металла и оргстекла с применением малобазовых тензодатчиков (база 0.8 мм) /3, 6/.

Тензодатчики располагались попарно в опасных точках берега НО на концах одного диаметра в осевом и окружном направлениях для исключения влияния изгиба из-за перекоса в захватах и отклонений приложенной силы от центральной оси. Растяжение проводилось до величины деформаций _x = 0.8%, при которой датчики начинали выходить из строя. Построена диаграмма - с упругопластическими зависимостями, из которой получены модуль упругости и диаграмма "интенсивность касательных напряжений - интенсивность деформаций сдвига" (кривая Т - Г). По результатам измерений определяются главные деформации в исследуемых точках, далее величины Г и Т (из диаграммы простого растяжения) и напряжения. Полученные экспериментальные значения ККН были выше расчетных для односторонней лунки, вычисленных по МКЭ без учета изгиба из плоскости НО. Результаты расчета и эксперимента для двусторонней лунки согласуются лучше чем для односторонней.

Экспериментальные данные для двусторонней и односторонней лунок показывают существенное влияние изгиба из плоскости НО на уровень напряжений (рис. 12).

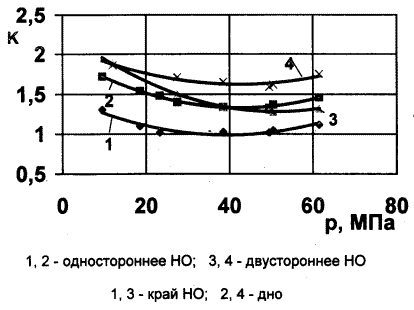
Рис. 12

3. Разработка КЭМ для элемента конструкции с НО

Формирование КЭ сети

Вокруг НО из тонкостенной конструкции выделяется прямоугольный элемент с заданными толщиной, размерами в плане и радиусами кривизны поверхности. Элемент рассматривается как трехмерное упругое тело и предполагается что:

- на вертикальных гранях элемента действуют нормальные и касательные напряжения, определяемые из решения соответствующей упругой задачи без учета влияния НО;

- НО имеет одну из идеализированных форм в плане: круговую, эллипсоидальную, прямоугольную, прямоугольную со скругленными углами;

- в окрестности НО имеется трехмерная область, в которой механические характеристики материала отличаются от характеристик принятых для всего элемента; ее наличие обусловлено физико- химическими процессами при образовании НО (наклеп, коррозия и т.д.);

- рассматриваемый трехмерный упругий элемент с НО имеет входящие прямые углы, в окрестности которых характеристики НДС могут принимать экстремальные значения, а напряжения ограничиваются соответствующими условиями текучести.

При формировании сети КЭМ учитывалось, что в окрестности НО сеть имеет сгущение в плане, согласованное с градиентом поля напряжений, а поверхностные нагрузки разложены по функциям формы КЭ.

Для заданной топологии сети сопоставляются решения с учетом и без учета НО для оценки влияния разбивки. Далее, путем численного эксперимента, формируется приемлемая по ресурсам трехмерная КЭМ, адекватная принятой расчетной схеме и полю напряжений. Сходимость подтверждается последовательным пересчетом с увеличением количества узлов сети. При формировании КЭМ используется интерактивная система управления разбивкой. В блок подготовки данных вводятся геометрические и механические характеристики модели, а генерация КЭМ выполняется по специальным для данного объекта правилам.

Конструирование КЭМ для пластины с НО

Рассматриваются пластины с круговыми цилиндрическими НО двух видов. Первое -имеет входящий угол равный 90° , второе- блюдцеобразное, с зачисткой входящего угла по заданному радиусу R. Эти модели охватывают весьма широкий класс несквозных повреждений. Первая модель позволяет оценивать максимальную величину сдвиговых напряжений _rz и локального прогиба, вызываемых повреждением, вторая- оценивать влияние зачистки на величину КН.

В качестве элемента конструкции принимается квадратная пластина с центрально расположенным НО. В силу двойной симметрии моделируется четверть пластины. Граничные условия имеют вид:

Для оценки качества моделирования в качестве тестовой использовалась КЭМ для задачи Кирша. Параметры разбивки подбирались так, чтобы узловые нагрузки хорошо "растекались" по элементам. На тестовой КЭМ выбиралась величина стороны квадрата

обеспечивающая существование зоны не возмущенной отверстием и узловыми нагрузками. Проводилось сопоставление полученных численных решений с известными аналитическими для различных относительных размеров и свойств КЭ. КЭМ пластины cо сквозным отверстием и ее разделение на подконструкции показана на рис. 13.

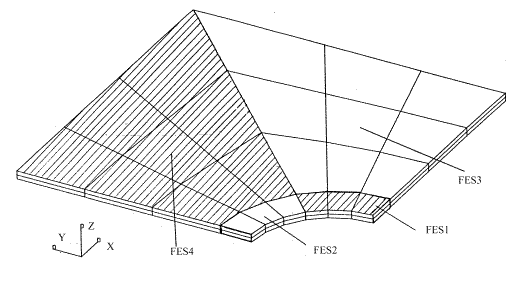
Рис. 13

При моделировании цилиндрического НО значительную сложность представляет подбор параметров разбивки "дна" НО. Если "дно" разбивается на клиновидные объемные КЭ, то при сгущении разбивки по окружности получаются удлиненные элементы и качество моделирования не улучшается. Необходимо также учитывать характер изгиба пластины, который зависит от радиуса и относительной глубины НО. Разбивка подбиралась таким образом, чтобы имелась монотонная сходимость решения при условии, что более подробная разбивка проводится в окрестности контура НО. КЭМ пластины с использованием в разбивке НО клиновидных объемных КЭ и разделение пластины на подконструкции представлены на рис. 14. Сгущение разбивки позволяет оценить сходимость решения на данной КЭМ.

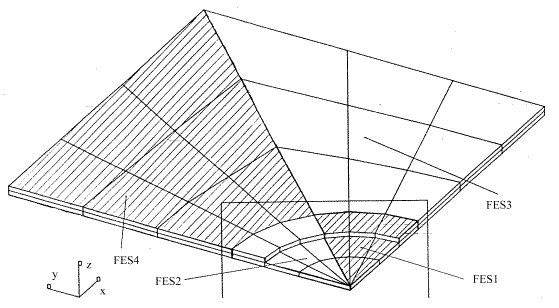
Рис. 14

КЭМ пластины для случая цилиндрического НО с закругленными входящими углами (зачисткой) представлены на рис. 15, 16. Они имеют различные структуры разбивки. Первая модель (рис. 15) является относительно простой, имеет однослойную разбивку с использованием клиновидных объемных КЭ для приполюсной зоны НО. Вторая КЭМ (рис. 16) имеет более сложную разбивку и не содержит клиновидных элементов. Центральная часть "дна" моделируется прямоугольными элементами. Эта модель допускает исследование НДС с учетом изменения свойств материала, примыкающего к НО и доработку сети путем изменения размеров составляющих КЭМ в плане. Фрагменты разбивок для выделенных на рис 15, 16 зон зачистки, соответствующие первой и второй моделям, показаны на рис. 17, 18.

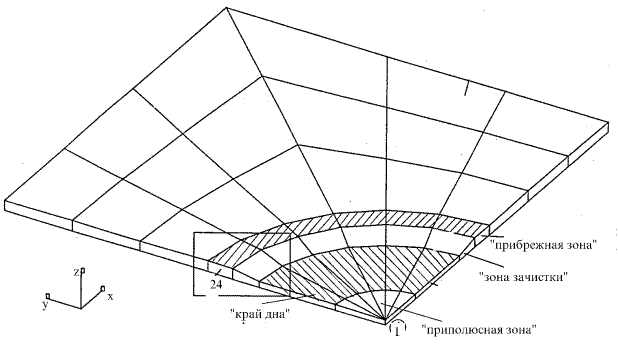
Рис. 15

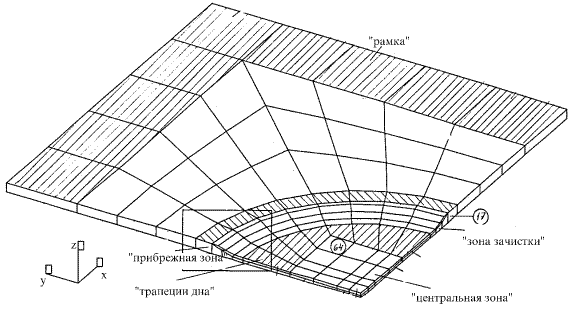
Рис. 16

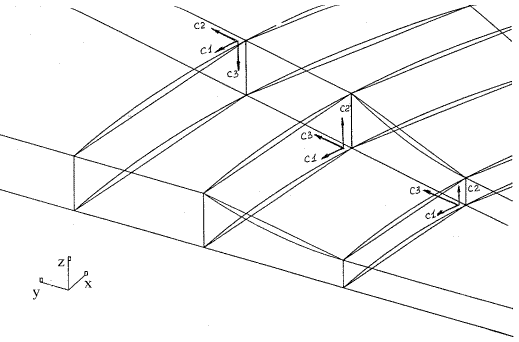
Рис. 17

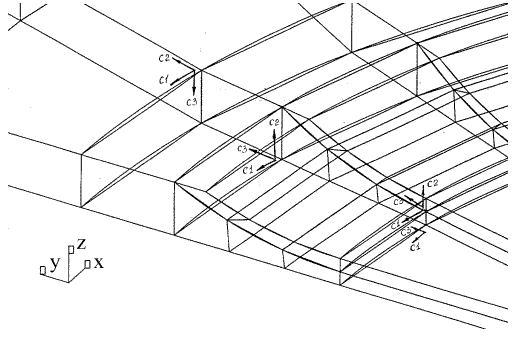
Рис. 18

ВЫВОДЫ

1. Проведен анализ и обобщение исследований НДС в зоне НО и показано, что:

- основными факторами, определяющими величину ККН, являются относительные величины и =d/(h-h₁);

- аналитическое решение задач оценки параметров НДС в зоне НО весьма сложно даже в упругой постановке; существующие аналитические решения получены для бесконечной пластины с полусферическим НО;

- использование МКЭ является наиболее эффективным путем получения оценок параметров НДС для конструкции с НО; возможность получения корректных результатов по ККН в зоне НО зависит от качества выбранной технологии МКЭ;

- наиболее изучено НДС около сферического НО, для оценки которого разработаны программы для решения осесимметричной задачи, а также плоской и объемной задач; построено математическое обеспечение для комплексного исследования повреждений типа НО многослойных тонкостенных конструкций на базе специализированных КЭ;

- известные расчетные оценки напряжений для цилиндрического НО без скругления имеют существенный разброс и непригодны для практического использования; могут быть использованы экспериментальные данные и оценки для НО с регулярным профилем.

2. На основе объемных КЭ большой размерности разработаны КЭМ пластины с цилиндрическим НО, позволяющие оценивать величину КН и локального прогиба при наличии входящего угла, а также влияние зачистки повреждения на величину КН.

3. Разработана модель, учитывающая изменение свойств материала, примыкающего к НО и доработку КЭ сети путем изменения размеров составляющих КЭМ в плане.

Список литературы.

1. Черепанов Г.П. Механика хрупкого разрушения.- М.: Наука, 1976.- 640 с.

2. Fujita T., Sadaysu T., Tshohida F., Hakahara I. Stress concentration due to hemisperical pit at a free surface of a thick plate under all- round tension. // Bull. ISME. -1978, 21, ╧ 154.- p. 561 - 565.

3. Сухинин В.П., Лежнева А.А. и др. Концентрация напряжений в пластинах с местными утонениями. // Проблемы прочности. - 1986, ╧ 3. -c. 91-93.

4. Раймонд Э.Д., Шиганов Э.В. Экспериментальное исследование влияния местных утонений металла на прочность цилиндрических оболочек.// Проблемы прочности. - 1974, ╧ 4.- с. 117 -120.

5. Необедрин Ю. А., Масленок Б.А. и др. Численное исследование в местах осесимметричных утонений пластин и оболочек. // Проблемы прочности. - 1981, ╧ 1.- с. 18-21.

6. Лежнева А.А., Мелерович Г.М., Якушина Г.М., Герман Н.М. Влияние местных утонений на напряженное состояние растягиваемых пластин.// Прочностные и динамические характеристики машин и конструкций. Межвуз. сб. - Пермь, 1988.- с. 25-31.

7. Мороз Н.Г., Гудов В.И. Концентрация напряжений в зоне несквозного круглого отверстия в одноосно растянутой толстой пластине. // Прикл. механика. - 1986, ╧ 5. -с.119 -121.

8. Ferry F., Bauce P., Taupin P. Analysis of primary membranstress in pipe attached by local under thickness disscountinuity. // Transactions of Int. Conf. of Struct. Mech. in reactor technology, Amsterdam, 1985. -p. 295 - 300.

9. Chandhuri Rear A. Stress concentration around a part - trough hole weaking a laminate plate. // Computers and structures. -1987, 27, N 5.- p. 601- 609.

10. Chandhuri Rear A. A degenerate triangular shell with constant cross- sectional warping. // Computers and structures. -1988, 28, N 3.- p. 315 - 325.