В данной статье рассматривается возможность моделирования подстилающей поверхности для радиолокационных систем с доплеровским обужением луча на основе информации о той же поверхности, полученной в оптическом диапазоне. Моделирование осуществлялось в системе координат, совпадающей с системой координат изображения в оптическом диапазоне, где направление носителя совпадает с ориентацией оптического изображения, что позволило получить модель изображения подстилающей поверхности в радиодиапазоне с максимальной точностью при прочих равных условиях. Приведены результаты моделирования растровых изображений при различных азимутальных углах отклонения диаграммы направленности (ДН) антенны радиолокационной системы (РЛС) носителя. Рассматривается медианная фильтрация в качестве предобработки изображения для его последующего анализа.

Решение задачи картографирования и распознавания подстилающих поверхностей и объектов на них в любых погодных условиях днем и ночью возможно при применении радиолокационных методов. При этом набор необходимой информации, получаемый экспериментально, непосредственно в радиодиапазоне, требует выполнения большого объема сложных и дорогостоящих полетов в разных климатических условиях и в различных регионах Земли. В связи с этим представляет значительный интерес построение моделей подстилающей поверхности для РЛС на основе информации, получаемой в оптическом диапазоне с помощью искусственных спутников Земли (ИСЗ), либо при помощи аэрофотосъемки. Указанная оптическая информация обычно формируется в условиях, обеспечивающих наиболее точное воспроизведение подстилающих поверхностей и объектов на них.

Применение оптики обусловлено в первую очередь хорошим потенциальным пределом разрешения, который, как известно, в любом диапазоне волн определяется длиной волны.

Таким образом, актуальна задача разработки методологии создания моделей подстилающих поверхностей для РЛС с доплеровским обужением луча и синтезированием апертуры на основе информации, получаемой о них в оптическом диапазоне. Такой подход может быть использован для построения радиолокационных моделей в различных диапазонах радиоволн, например, в сантиметровом, миллиметровом, дециметровом диапазонах, что существенно для решения задач распознавания и идентификации объектов с помощью различных датчиков, работающих в указанных диапазонах.

В данной статье предлагается подход к построению радиолокационных моделей на основе оптических изображений. Исходным является оптическое изображение, преобразованное в цифровую форму с фиксированной величиной элемента разрешения, инвариантного к его положению по углу и дальности. Это изображение, кадр прямоугольной формы, формируется в географической системе координат с определенной ориентацией. Радиолокационная модель формируется также в географической системе координат, где направление носителя совпадает с ориентацией (с одной из осей) кадра оптического изображения. Это позволяет получать радиолокационные модели, с наибольшей точностью воспроизводящие исходные оптические при прочих равных условиях.

В настоящее время существует много задач гражданского и военного назначения, при которых информация об объектах получается на основе датчиков различной физической природы, в том числе в различных областях спектра электромагнитных излучений.

С целью повышения доверия к получаемым в ходе решения задачи картографирования результатам возникает необходимость сопоставления результатов, полученных от различных источников и/или в различных спектральных диапазонах и при различных методах обработки информации. Здесь существует проблема отождествления объектов в различных диапазонах длин волн, которая может быть решена путем разработки аппаратуры, учитывающей эти аспекты.

В частности, возможность совместной обработки изображений L-диапазона, полученных радиолокационной системой с синтезированной апертурой, и спектрозональных снимков оптического мультиспектрального сканирующего устройства для классификации лесных сообществ была рассмотрена в статье [1] . На основе результатов совместной обработки изображений, полученных в радио и в оптическом диапазонах был сделан вывод о лучшем разделении лесных массивов и выделении лесов без листвы (хвои).

Проблемы физической доступности исследуемого объекта в определенном спектральном диапазоне в конкретных условиях получения информации (самолетная разведка местности территории иностранного государства), минимизация затрат на основе критерия эффективности при заданной стоимости получения информации, способствуют развитию и совершенствованию задач моделирования. Доверие к результатам моделирования, а именно к корректности методологии и исходным данным, к источнику сравнения, играет большую роль в этом процессе.

Степень соответствия процесса моделирования реальным данным определяется не только приближением к реальным/опытным данным используемых конкретных моделей составляющих параметров, но и их числом или сложностью построения модели в целом. Наиболее важную роль в процессе моделирования играет степень соответствия моделей зависимости ЭПР конкретных типов объектов от изменяющихся параметров режима обзора (например настильного угла , рис. 1.) . При моделировании любого сложного по своей структуре процесса возможно лишь определенное приближение. Наиболее надежным способом проверки приближения моделирования данного процесса к реальным данным является, естественно, проведение конкретных измерений и доводка на их основе моделей изменения ЭПР конкретных объектов и структуры модели конкретной системы обработки принимаемых данных. Результаты рассматриваемого моделирования изображения подстилающей поверхности и объектов на ней не претендуют на высокую степень соответствия конкретным типам объектов и лишь служат основой для построения и улучшения данной процедуры. Развитие и уточнение рассматриваемой процедуры видится как процесс постепенного усложнения модели до степени нужной в конкретной задаче (учет влияния боковых лепестков ДН антенны, характера шумов и помех как среды распространения сигнала, так и конкретно используемой аппаратуры и т.д.).

Исходными положениями при моделировании являются:

а) исходное оптическое изображение:

1. Оптическая модель строится как многоуровневое квантование исходного изображения при преобразовании его в цифровую форму (файл растрового изображения) с выбранной фиксированной величиной элемента разрешения.
2. На исходном оптическом изображении выбирается размер пространственного окна, которому будет поставлено в соответствие радиолокационное изображение. Для описания пространственного окна вводится предельное значение элемента разрешения (например 1м х 1м), в единицах которого выражается фиксированный в данной задаче элемент разрешения (например 10м х 10м).

б) Исходные данные для формирования модели радиолокационного изображения показаны на рис.1 и 2, а также в приложении:

1. Исходные данные для расчета размеров сечения подстилающей поверхности диаграммой направленности антенны РЛС носителя и для расчета элемента разрешения, формируемого на основе углового разрешения и разрешения по дальности, и выраженного в единицах предельного разрешения: настильный и азимутальный углы, ширина ДН антенны по уровню 0.7, ширина полосы доплеровского фильтра, высота и скорость полета носителя РЛС. При этом носитель РЛС совершает полет в направлении, совпадающем с ориентацией выбранного пространственного окна на оптическом изображении (последнее замечание не является обязательным условием, а лишь служит цели максимального соответствия получаемых результатов при прочих равных условиях).
2. Исходные данные для расчета мощности, отраженной от подстилающей поверхности: диапазон частот передатчика РЛС носителя, мощность передатчика, коэффициент усиления антенны.
3. Исходные данные, используемые в моделях изменения удельной эффективной поверхности рассеяния (УЭПР) конкретных типов подстилающих поверхностей: коэффициент возмущения морской поверхности* (для всех моделей общим является такой параметр как настильный угол).

В данной статье, как в оптике, так и в радиолокационной модели изображения подстилающей поверхности, инструментальные ошибки, возможные при формировании и обработке информации, не учитываются, что не следует рассматривать как недостаток, а как модель с максимальной потенциально достижимой точностью при соответствующих разрешениях и степени сложности модели в целом. В каждом конкретном случае, при необходимости, в модели могут быть учтены представляющие интерес ошибки.

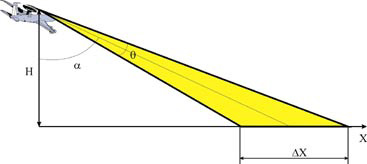
Рис.1. Картографирование в режиме реального луча

≈ настильный угол;

≈ ширина ДН антенны по уровню 0.7;

Н ≈ высота носителя;

Х ≈ приближенная протяженность сечения ДН антенны плоскостью подстилающей поверхности.

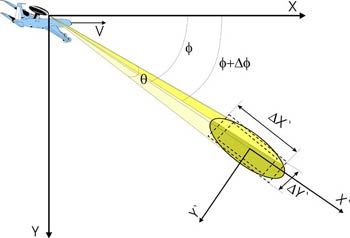
Рис.2. Картографирование с угловым разрешением

V ≈ скорость носителя (имеется ввиду, что носитель летит с постоянной скоростью в пределах необходимогарантированного интервала времени обзора);

- азимутальный угол;

≈ элементарный угол, соответствующий доплеровскому разрешению

Разрешение по дальности определяется шириной спектра излучаемых сигналов. Угловое разрешение определяется углом . Оно линейно зависит от ширины полосы доплеровского фильтра, длины волны радиолокационного сигнала, обратно пропорционально скорости носителя РЛС и синусу угла отклонения ДН антенны РЛС.(1)

     (1)

В процессе моделирования осуществляется сопоставление мощностей, отраженных от объектов поверхности, определенным интенсивностям в аналогичных сегментах оптического изображения. Данные мощности рассчитываются в соответствии с уравнением радиолокации и усредняются по элементам разрешения (имеется ввиду "совокупный" элемент разрешения, определяемый как разрешением по дальности, так и угловым разрешением). При моделировании типов подстилающих поверхностей использованы модели, описанные в статье [2] .

Структура алгоритма моделирования представлена в приложении.

На первом этапе задаются основные исходные параметры (см. приложение). В дальнейшем они могут меняться в определенных пределах, ограниченных, главным образом, исходными параметрами кадра оптического изображения (его размерами), изменяя тем самым получаемые результирующие изображения радиолокационной модели подстилающей поверхности с объектами.

Следующим шагом является расчет размеров сечения (X`, Y`) аппроксимированной диаграммы направленности антенны РЛС носителя подстилающей поверхностью, исходя из очевидных геометрических соотношений (рис.1 и 2).

Также рассчитывается соответствующее исходным данным угловое разрешение антенны РЛС носителя, в то время как разрешение по дальности вводится напрямую.

На третьем этапе осуществляется задание моделей изменения удельных отражающих поверхностей рассеяния (УЭПР) от ряда параметров, как общих (настильный угол), так и частных, присущих конкретным типам поверхностей (например, для морской поверхности учитывается коэффициент спокойствия). Данный этап моделирования является определяющим, так как именно на его основе ведется классификация типов поверхностей по отраженной мощности от элемента разрешения, сформированного угловым разрешением и разрешением по дальности антенны РЛС носителя, и выраженного в единицах предельного разрешения.

В задаче картографирования и идентификации объектов очень важную роль играет выбор конкретных моделей (моделей изменения ЭПР объектов, моделей распространения волн в конкретных сегментах среды (тропосфера, ионосфера и т.д.) или учитывающих погодные факторы и др.). Предложенный алгоритм построения модели не ограничивает учет как можно большего влияния этих факторов, особенно касающихся сложности моделей изменения ЭПР объектов. Достигаемая детализация изображений ограничивается возможностями модели радиолокационной системы носителя, а также зависит от количества используемых моделей типов поверхностей и объектов на них.

После "загрузки" оптического аналога (окна растрового изображения или файла растровой графики) происходит его анализ на основе ранее проведенных этапов (см. приложение).

Этот анализ осуществляется на основе расчета отраженной мощности от элементов разрешения по основному уравнению радиолокации, как зависимости от УЭПР, на основе выделения информации о цветовой градации элемента разрешения на оптическом изображении, соответствующего рассчитанному для радиолокационной модели.

На конечном этапе проводится визуализация результатов моделирования и их сохранение (двумерный массив отраженных мощностей, записанный в бинарный файл) для последующей обработки, например фильтрации и распознавания. Собственно данный этап идет синхронно с предыдущим, т.е. с анализом оптического изображения на основе сопоставления конкретной модели типа подстилающей поверхности определенной интенсивности оптического аналога.

Далее приведены некоторые результаты моделирования процесса картографирования земной поверхности. Со стремлением азимутального угла к 90⁰ увеличивается угловое разрешение и, как следствие, общее разрешение, тем самым лучше выявляя форму малоразмерных объектов (область А рис.3.). При этом некоторые мелкие, сравнимые с разрешающей способностью, объекты могут не проявляться, попадая на границы сегментов разрешения и усредняясь в них. Для уменьшения влияния таких эффектов необходимо несколько смещать кадр обзора земной поверхности по обоим координатам, либо использовать перекрытие окон анализа, определяемых аппроксимированным сечением ДН антенны РЛС плоскостью земной поверхности. Рис.3 по сути характеризует режим реального луча. Для рассмотренных случаев настильные углы равнялись 20⁰ при высоте полета носителя 2 км и скорости 200 м/с. Ширина ДН антенны по уровню 0.7 бралась 2.4⁰.Разрешение по дальности бралось 5м, угловое разрешение изменялось от 76 м (режим реального луча) до 4м (азимутальный угол 90⁰) при полосе доплеровских фильтров 10 Гц. На всех фрагментах изображения присутствуют только три типа поверхности: лес, травяной покров и водная поверхность. Как уже упоминалось выше данные модели упрощены и в них не учтены, а точнее сказать не разделены, такие важные особенности, как подтип поверхности (смешанный, хвойный, мелколиственный типы лесных стаций), различные стадии вегетационного периода растений, покрывающих тот или иной фрагмент поверхности, временные изменения и внутренняя структура, присущие отдельным типам объектов, влияние климатических факторов, особенности рельефа и т.д. В дальнейшем планируется дополнение и расширение данных моделей.

Ниже приводятся: оптический аналог (опорный снимок рис.3а, сведенный к трехуровневой градации интенсивности) и некоторые результаты моделирования процесса картографирования.

Фрагменты изображения рис.3 имеют размер 420х366 пикселей. Каждый пиксель эквивалентен 1м. Двумерный элемент разрешения на изображении, представляющем радиолокационную модель, имеет несколько пикселей, число которых определяется как разрешением по дальности, так и угловым разрешением. Разрешение оптического аналога равно предельному разрешению (1 пиксель). Направление полета носителя параллельно вертикальному ребру рис.3.

С точки зрения выявления основных черт карты местности без учета сравнительно мелких объектов рис.3д дает уже достаточное разрешение.

Канва вокруг водной поверхности объясняется усреднением фрагментов разрешения. Она присутствует на границах любых типов поверхности, просто в случае границы лесной и луговой стаций, канва оказалась отождествленной с лесным типом. Область Б рис.3(с-ж) , на которой реально должен находиться один из речных рукавов, вследствие пиксельного усреднения (ширина речного рукава меньше сегмента разрешения, определяемого несколькими пикселями) оказалась отождествлена с иным типом поверхности.

Для надежного разрешения, а затем и идентификации относительно мелких объектов, сравнимых с сегментами разрешения, необходима такая фрагментация исследуемых объектов, которая обеспечивает как можно меньшие искажения на границах данных объектов, если не существует каких либо других аспектов идентификации.

5. Медианная фильтрация получаемых изображений

В предыдущих разделах данной статьи шла речь о моделировании изображений. При этом оптический аналог считался либо идеальным, либо пренебрежимо мало зашумленным.

Реальные изображения, сформированные различными информационными системами, искажаются действием помех в той или иной степени. Это затрудняет как их визуальный анализ, так и автоматическую обработку. При решении некоторых задач обработки изображений в роли помех могут выступать те или иные компоненты самого изображения. Так, при анализе снимка земной поверхности может стоять задача определения границ между ее отдельными участками ≈ лесом и полем, водой и сушей и т.п., что особенно существенно для процесса распознавания объектов по их структуре. С точки зрения этой задачи отдельные детали изображения внутри разделяемых областей могут являться помехой. Это особенно относится к изображениям, получаемым от радиолокационных источников инфомации, когда помехи могут нарушить структуру отдельных объектов изображения и/или исказить их тип по классификации, либо существует множество относительно мелких по-сравнению с целью объектов.

Ослабление действия помех достигается фильтрацией. При фильтрации яркость (либо определенный цвет в случае цветного изображения) каждой точки исходного изображения, искаженного помехой, заменяется некоторым другим значением яркости (или цвета), которое признается в наименьшей степени искаженным помехой. Изображение часто представляет собой двумерную функцию пространственных координат, которая изменяется по этим координатам медленнее (иногда значительно медленнее), чем помеха, также являющаяся двумерной функцией. Это позволяет при оценке полезного сигнала в каждой точке кадра анализировать некоторое множество соседних точек, имея ввиду определенную схожесть сигнала в этих точках. В других случаях, наоборот, признаком полезного сигнала являются резкие перепады яркости. Однако, как правило, частота этих перепадов относительно невелика, так что на значительных промежутках между ними сигнал либо постоянен, либо изменяется медленно. И в этом случае свойства сигнала проявляются при наблюдении его не только в локальной точке, но и при анализе ее окрестности.

Все линейные алгоритмы фильтрации приводят к сглаживанию резких перепадов яркости изображений, прошедших обработку. Линейные процедуры являются оптимальными при гауссовском распределении сигналов, помех и наблюдаемых данных [3] . Реальные изображения, строго говоря, не подчиняются данному распределению вероятностей. Причем, одна из основных причин этого состоит в наличии у изображений разнообразных границ, перепадов яркости, переходов от одной текстуры к другой и т. д. Поддаваясь локальному гауссовскому описанию в пределах ограниченных участков, многие реальные изображения в этой связи плохо представляются как глобально гауссовские объекты. Именно это и служит причиной плохой передачи границ при линейной фильтрации.

Часто встречаются изображения, искаженные помехами других типов. Одной из них является импульсная помеха. При ее воздействии на изображении с оттенками серого цвета наблюдаются белые или (и) черные точки, хаотически разбросанные по кадру. Применение линейной фильтрации в этом случае часто малоэффективно - каждый из входных импульсов ( по сути - дельта-функция) дает отклик в виде импульсной характеристики фильтра, а их совокупность способствует распространению помехи на всю площадь кадра.

Лучшие результаты для сохранения перепадов оттенков, различных границ и локальных пиков яркости на зашумленных изображениях может дать применение медианной фильтрации, предложенной Дж. Тьюки в 1971 г. для анализа экономических процессов [3] .

При применении медианного фильтра (МФ) происходит последовательная обработка каждой точки кадра, в результате чего образуется последовательность оценок. Обработка в различных точках независима.

При медианной фильтрации изображений используется двумерное окно (апертура фильтра), обычно имеющее центральную симметрию, при этом его центр располагается в текущей точке фильтрации. На рис.4 показаны три примера вариантов окон в виде прямого и диагонального крестов и в виде прямоугольника. Размеры апертуры относятся к параметрам, оптимизируемым в процессе анализа эффективности алгоритма. Отсчеты изображения (пиксели черного цвета), оказавшиеся в пределах окна, образуют рабочую выборку текущего шага.

а) прямой крест 3х3	б) диагональный крест 3х3	в) квадрат 3х3
Рис. 4. Примеры окон (апертур) при медианной фильтрации

Двумерный характер окна позволяет выполнять, по существу, двумерную фильтрацию, поскольку для образования оценки привлекаются данные как из текущих строки и столбца, так и из соседних. Если импульсная помеха не является точечной, а покрывает некоторую локальную область, то она также может быть подавлена. Это произойдет, если размер этой локальной области будет меньше, чем половина размера апертуры МФ. Поэтому для подавления импульсных помех, поражающих локальные участки изображения, следует увеличивать размеры апертуры МФ.

Исследования подавления шума при помощи медианной фильтрации [4] показывает, что ее эффективность при решении этой задачи ниже, чем у линейной фильтрации. Рис.5 б и с демон-стрируют некоторые результаты медианной фильтрации зашумленного изображения (Рис.5 а).

Рис.5 Медианная фильтрация зашумленного изображения.

Применительно к фильтрации кадров изображения, полученных радиолокационным методом или смоделированных, медианная фильтрация может оказаться полезной для дальнейшего процесса распознавания как попытка устранения лишней или мешающей информации вкупе с сохранением основных черт формы интересующих объектов. Результаты экспериментов над Рис.3 ж в качестве исходного изображения, иллюстрирующие работу МФ, приведены на рис.6.

Как видно по Рис.6 из представленных результатов фильтрации наилучшим оказался Рис.6 ж, если считать интересующими крупные объекты области В. При сохранении их формы отфильтровались все мелкие детали. В данном случае применялись только три формы апертуры МФ, возможны и другие варианты апертур. В конечном итоге на выбор конкретной апертуры влияют характер и степень "зашумленности" изображения, влияние МФ на форму интересующих объектов и скорость обработки (чем меньше количество анализируемых пикселей в каждом такте процедуры фильтрации, тем выше скорость).

Вместе с тем, как говорилось выше, что и демонстрируют рис. 5 и 6, медианная фильтрация в меньшей степени сглаживает границы изображения, чем любая линейная фильтрация, сохраняя контраст и характер границ и перепадов интенсивностей объектов изображения. Механизм этого явления очень прост и заключается в следующем. Если предположить, что апертура фильтра находится вблизи границы, разделяющей светлый и темный участки изображения, при этом ее центр располагается в области темного участка. Тогда, вероятнее всего, рабочая выборка будет содержать большее количество элементов с малыми значениями яркости, и, следовательно, медиана будет находиться среди тех элементов рабочей выборки, которые соответствуют этой области изображения. Ситуация меняется на противоположную, если центр апертуры смещен в область более высокой яркости. Но это и означает наличие чувствительности у МФ к перепадам яркости.

1.Показана возможность моделирования изображений земной поверхности и объектов на ней в радиодиапазоне на основе изображений, полученных в оптическом диапазоне. При этом показано влияние особенностей обработки информации в радиодиапазоне на форму и точность воспроизведения объектов, а также на принадлежность к тому же типу, который имеется в действительности (на оптическом изображении). Так, уже упоминавшаяся ранее область Б рис.3 с ростом азимутального угла луча воспроизводится все точнее и точнее, однако при принятых разрешающих способностях по дальности и углу азимута эта область оказалась отнесенной не к речному рукаву, а к лесному массиву такой же формы. При более точных моделях типов объектов, либо при многоканальном картографировании эта неоднозначность уменьшится.

2. В данной статье система координат носителя при моделировании совпадает с географической системой координат, в которой получены оптические изображения; направление носителя совпадает с ориентацией оптического изображения. Такой подход обеспечивает наибольшую точность воспроизведения изображения в радиодиапазоне подстилающей поверхности с объектами по отношению к оптическому. На основе полученной таким образом модели изображения в радиодиапазоне возможно построение изображений при любых курсовых углах носителя, с выявлением получаемых при этом точностей воспроизведения соответствующих объектов.

3. Для исключения потери деталей оптического изображения в получаемом радиолокационном, которая обусловлена попаданием этих деталей на границы сегментов разрешения, возможно осуществлять моделирование с частичным наложением окон, аналогичным наложению окон при обработке сигналов [5] .

4. В зависимости от процесса дальнейшей обработки изображений, возможна соответствующая оптимизация медианной фильтрации. Так, например, в случае распознавания объектов определенного размера, либо по-крайней мере одного порядка, выбором соответствующей апертуры МФ возможно не только подавление шума на изображении, но и непредставляющих интерес деталей меньшего размера. То же самое может относиться и к задаче привязки изображения или выделения характерных опорных фрагментов. В выборе апертуры МФ следует обязательно учитывать возможные искажения формы представляющих интерес объектов, а также преобладающую структуру этих объектов, при наличии априорных сведений о ней. Так, в случае "сеточной" структуры объектов (населенные пункты; ирригационные каналы; площади, насыщенные разного рода коммуникациями в виде линий электропередач, взлетно-посадочных полос, и т.д.) применение МФ с крестообразной апертурой может оказаться более выгодным по-сравнению с остальными. Кроме того, возможно применение комбинации МФ и наложения результатов фильтрации с целью уменьшения "потерь" формы объектов изображения, что однако снижает скорость обработки; либо использование соответствующих апертур, способных как можно лучше учитывать особенности структуры изображений, если такие имеются.

Приложение

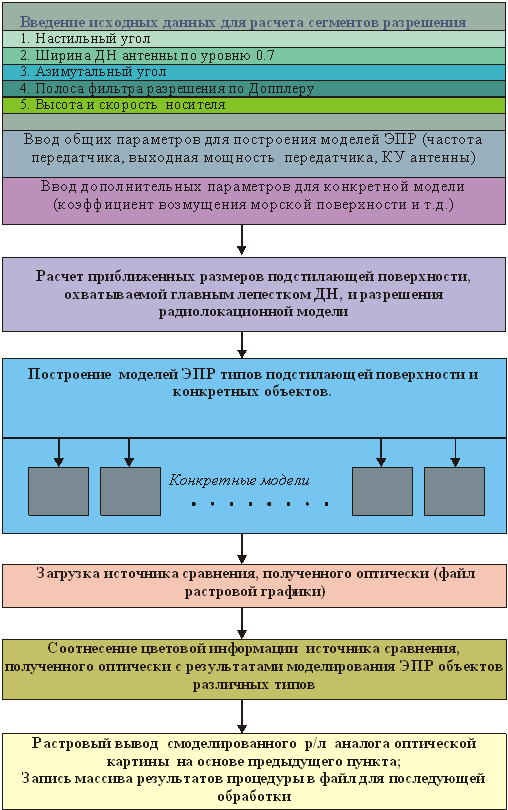
Алгоритм процедуры картографирования

Список литературы

1. Радиотехника и электроника.≈ 1988, том 43, ╧9. ≈ с.1070-1075

2. R.Barton. Targets and interference, 1990. - l.122-139.

3. Быстрые алгоритмы в цифровой обработке изображений. /Под ред. Т.С. Хуанга. - М.: Радио и связь, 1984.≈43с.

4. Грузман И.С.,Киричук В.С., Косых В.П.,Перетягин Г.И., Спектор А.А. Цифровая обработка изображений в иформационных системах. Учебное пособие.- Новосибирск: НГТУ, 2000. √ 168с.

5. Марпл С.П. Цифровой спектральный анализ и его приложения. М: Мир,1990.≈112с.