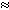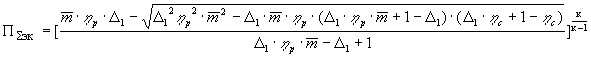УДК 629.7.036.001(07.58)
Исследование термодинамического цикла
двухкамерного турбореактивного двигателя
В.Л. Письменный
Рассмотрены термодинамические циклы
идеального и реального двухкамерного турбореактивного двигателя. Дан анализ
их особенностей и принципов выбора оптимальных параметров. Показаны
теоретические возможности получения различных удельных тяг и удельных
расходов топлива двухкамерными турбореактивными двигателями.
В последнее время наблюдается тенденция к
существенному снижению степени двухконтурности
форсированных двухконтурных турбореактивных
двигателей (ТРДДФ), предназначенных для
многоцелевых сверзвуковых самолетов. Так,
например, двигатель, разрабатываемый в США по
программе ATF создания перспективного
истребителя, должен иметь температуру Тг*=1800
К, степень повышения давления Пк = 25 и степень двухконтурности m = 0,25.
Столь значительное снижение параметра m
объясняется повышением доли форсированных
режимов в общей наработке двигателей. В связи с
этим становится более выгодным понижать расходы
топлива на форсированных режимах, чем на
крейсерских, что возможно при значительном
снижении параметра m. В сложившейся ситуации
альтернативой двухконтурному форсированному
двигателю может стать двухкамерный
турбореактивный двигатель [1] (рис. 1), у которого
диапазон изменения удельных расходов топлива по
режимам существененно уже.
= 25 и степень двухконтурности m = 0,25.
Столь значительное снижение параметра m
объясняется повышением доли форсированных
режимов в общей наработке двигателей. В связи с
этим становится более выгодным понижать расходы
топлива на форсированных режимах, чем на
крейсерских, что возможно при значительном
снижении параметра m. В сложившейся ситуации
альтернативой двухконтурному форсированному
двигателю может стать двухкамерный
турбореактивный двигатель [1] (рис. 1), у которого
диапазон изменения удельных расходов топлива по
режимам существененно уже.
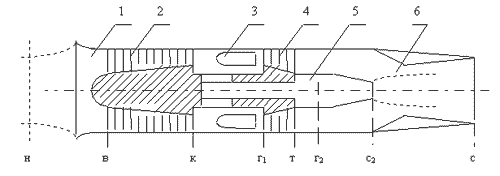
Рис. 1
Двухкамерный ТРД (ТРДК) состоит из входного
устройства 1, компрессора 2, основной камеры
сгорания 3, турбины 4, дополнительной камеры
сгорания 5, эжекторного сопла 6. При этом основная
камера сгорания 3 расположена между компрессором
2 и турбиной 4, а дополнительная камера сгорания 5
расположена между турбиной 4 и эжекторным соплом
6 и соединена с компрессором 2 каналом, проходящим
через вал двигателя. Эжекторное сопло 6 -
сверхзвуковое с регулируемым вторичным (внешним)
соплом и нерегулируемым первичным (внутренним)
соплом, являющимся продолжением камеры сгорания
5.
Работа двигателя осуществляется следующим
образом. Воздух из атмосферы через входное
устройство 1 поступает в компрессор 2 для сжатия.
Сжатый до заданного давления воздух делится на
два потока.
Первый поток поступает в основную камеру
сгорания 3, куда одновременно через форсунки
впрыскивается мелкораспыленное топливо.
Образующийся в результате сгорания газ
поступает на турбину 4, которая приводит во
вращение компрессор 2. Выходящий из турбины газ
поступает с дозвуковой скоростью во вторичное
сопло.
Второй поток через канал внутри вала поступает
в дополнительную камеру сгорания 5, куда
одновременно через форсунки впрыскивается
мелкораспыленное топливо. Образовавшийся в
результате сгорания газ истекает со звуковой
(сверхзвуковой) скоростью из первичного во
вторичное сопло.
В дозвуковой части вторичного сопла первый и
второй потоки движутся параллельно с ускорением,
практически, не перемешиваясь [2] . В критическом
сечении скорость первого потока достигает
скорости звука, после чего начинается смешение
потоков. На срезе сверхзвукового сопла скорости
истечения обоих потоков достигают максимальных
значений, что создает высокую удельную тягу.
Идеальный двухкамерный ТРД. Идеальным, с
газодинамической точки зрения, двухкамерным ТРД
можно считать двигатель, у которого работа
основного цикла в максимальной степени
передается дополнительному циклу, т.е.
выполняется условие: Пк = Пт, где Пк - степень повышения давления в
компрессоре; Пт - степень понижения давления на
турбине (здесь и дальше Пк и Пт
берутся по заторможенным параметрам). При этом:
- Газ идеальный (газовая постоянная Rг и
показатель адиабаты к = ср/сv остаются
неизменными).
- Потери в процессах сжатия, подвода тепла и
расширения отсутствуют.
Здесь и дальше будем рассматривать состояние
воздуха или продуктов сгорания в характерных
сечениях и за каждым агрегатом двигателя, в
котором происходит то или иное преобразование
энергии, и обозначать эти сечения индексами,
соответствующими агрегатам, за которыми
располагаются данные сечения (рис. 1).
ТРДК имеет два цикла: основной (рис. 2,а) и
дополнительный (рис. 2,б), изображенные в p-v
координатах, где кривые н-к, г1-с, г2-с▓
- адиабаты.
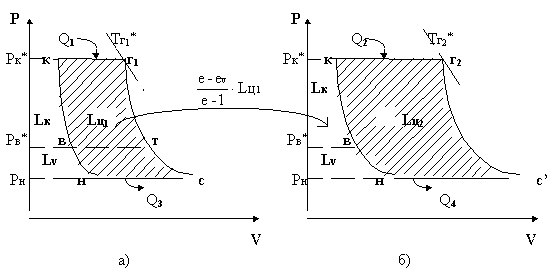
Рис. 2
Работа основного цикла в ТРДК (рис. 2.а) в общем
случае делится на две части:
- Работа, которая расходуется на сжатие рабочего
тела в дополнительном цикле.
- Работа, которая расходуется на увеличение
кинетической энергии рабочего тела в основном
цикле.
Работа основного цикла, приходящаяся на 1 кг
рабочего тела, определяется соотношением:
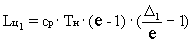 , (1)
, (1)
где 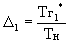 -
подогрев газа в основной камере сгорания,
-
подогрев газа в основной камере сгорания,
 - суммарная
степень сжатия.
- суммарная
степень сжатия.
Работа дополнительного цикла, приходящаяся на 1
кг воздуха, определяется соотношением:
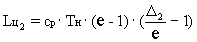 (2)
(2)
где 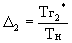 -
подогрев газа в дополнительной камере сгорания.
-
подогрев газа в дополнительной камере сгорания.
Суммарная работа обоих циклов (основного и
дополнительного) определяется из условия:
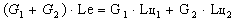 ,
,
где Le - суммарная работа циклов, приходящаяся на
1 кг рабочего тела,
G1, G2 - расходы рабочего тела
основного и дополнительного циклов,
откуда
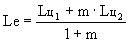 (3)
(3)
где m 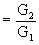 -
степень двухконтурности ТРДК.
-
степень двухконтурности ТРДК.
Степень двухконтурности m определяется из
условия равенства работ компрессора и турбины:
 , (4)
, (4)
где Lк - работа компрессора,
приходящаяся на 1 кг рабочего тела,
Lт - работа турбины, приходящаяся на
1кг рабочего тела.
В развернутом виде выражение (4) может быть
представлено как
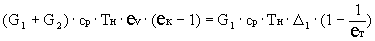 ,
,
где 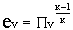 ;
; 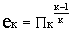 ;
; 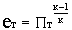 .
.
Откуда, принимая во внимание, что ет = ек и еv = е/ек,
получаем
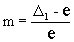 , (5)
, (5)
После подстановки (1), (2), (5) в (3) получаем
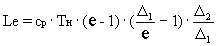 (6)
(6)
или 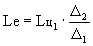
Таким образом, характер изменения суммарной
работы циклов, приходящейся на 1 кг рабочего тела,
в идеальном ТРДК определяется, как это видно из
полученного соотношения, характером изменения
работы основного цикла. Из чего следует:
- Оптимальная степень повышения давления в
идеальном ТРДК (при условии
 2=const)
определяется также как в идеальном ТРД, а именно:
eopt =
2=const)
определяется также как в идеальном ТРД, а именно:
eopt = 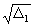 или
или
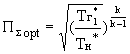 .
.
- Термический КПД двигателя определяется
известным соотношением
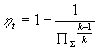 .
.- Максимальная работа циклов, которая
получается подстановкой еopt =
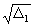 в (6), соответствует
величине:
в (6), соответствует
величине:
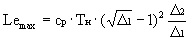 .
.
Для реальных подогревов (например,  1=5,5 и
1=5,5 и  2=10,5)
увеличение полезной работы ТРДК по отношению к
ТРД, как это следует из полученного для Lemax
cоотношения, составляет более 50%.
2=10,5)
увеличение полезной работы ТРДК по отношению к
ТРД, как это следует из полученного для Lemax
cоотношения, составляет более 50%.
С целью количественной оценки
предельных возможностей двигателя определим
основные удельные параметры идеального ТРДК в
условиях старта (Мп=0; Н=0).
Известно [3] , что работа цикла (циклов)
ВРД прямой реакции преобразуется в кинетическую
энергию реактивной струи, т.е.
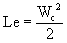 , откуда
, откуда 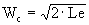 .
.
В условиях старта Pудо = Wc или 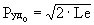 .
.
Заменяя Le, получаем
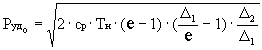 (7)
(7)
или 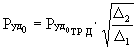 ,
,
т.е. удельная тяга идеального ТРДК (Н=0, Мп=0)
отличается от удельной тяги идеального ТРД в 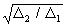 раз.
раз.
Подставляя в (7) eopt= 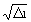 , определяем оптимальную
удельную тягу в условиях старта
, определяем оптимальную
удельную тягу в условиях старта
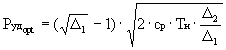 .
.
Для ср = 1,15 кдж/кг·град и Тн = 288 К,
соответственно:
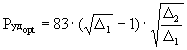 [дан·с/кг]. (8)
[дан·с/кг]. (8)
Известно [3] , что удельный расход топлива
определяется формулой
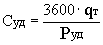 , (9)
, (9)
где 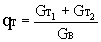 - суммарный относительный расход
топлива,
- суммарный относительный расход
топлива,
Gт1 = G1·qт1
- расход топлива через
основную КС,
Gт2 = G2·qт2 - расход топлива через
дополнительную КС.
Откуда 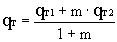
или 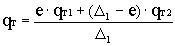 .
.
Из баланса энергий в основной КС имеем
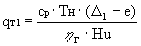 .
.
Из баланса энергий в дополнительной КС
имеем
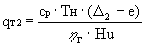 .
.
Тогда 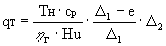 . (10)
. (10)
Подставляя (7) и (10) в (9), получаем
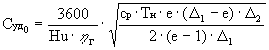 (11)
(11)
или 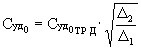 ,
,
т.е. удельный расход топлива в
идеальном ТРДК (Н=0, Мп = 0) отличается от удельного расхода
топлива в идеальном ТРД в 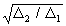 раз.
раз.
Таким образом, у идеального ТРДК
удельная тяга и удельный расход топлива в
стартовых условиях изменяются
пропорционально.
Подставляя в (11) eopt= 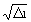 , определим
удельный расход топлива, соответствующий
оптимальной удельной тяге в условиях старта:
, определим
удельный расход топлива, соответствующий
оптимальной удельной тяге в условиях старта:
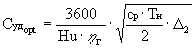 ,
,
который для определенности назовем
оптимальным удельным расходом топлива. Для ср
= 1,15 кдж/кг·град, Тн = 288 К,
Нu = 429000 кдж/кг·град, 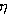 г = 0,98, соответственно:
г = 0,98, соответственно:
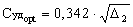 [кг/дан·ч] . (12)
[кг/дан·ч] . (12)
На рис.3 показаны оптимальные удельные
тяги и соответствующие им оптимальные удельные
расходы топлива для различных  1
и
1
и  2 в условиях старта.
2 в условиях старта.
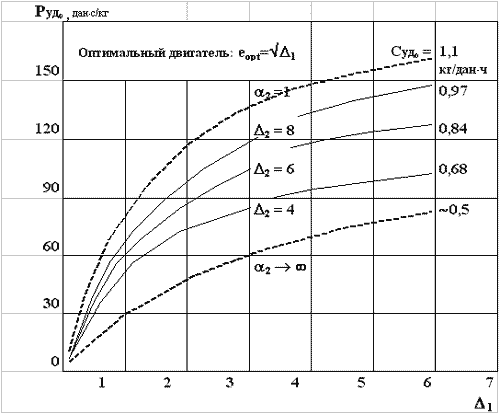
Рис. 3
Видно, что:
- Судopt идеального ТРДК не
зависит от подогрева
 1,
что является следствием равенства термических
КПД обоих циклов.
1,
что является следствием равенства термических
КПД обоих циклов.
- Предельные значения исследуемых
параметров ограничены энергетическими
возможностями дополнительной КС.
Из баланса энергий в дополнительной КС
следует
 2= e +
2= e + 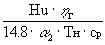 , (13)
, (13)
где 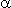 2 -
коэффициент избытка воздуха в дополнительной
камере сгорания.
2 -
коэффициент избытка воздуха в дополнительной
камере сгорания.
C учетом значений известных параметров
 2 = e +
2 = e + 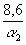 ,
,
Откуда, принимая во внимание eopt = 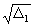 , для
, для 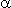 2
2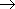
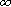 и
и
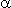 2 = 1 имеем
2 = 1 имеем
 2min=
2min= 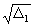 ;
;  2max=
2max= 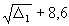 .
.
После подстановки  2min и
2min и 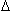 2max в (8) и (12) получаем
предельные значения:
2max в (8) и (12) получаем
предельные значения:
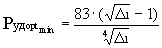 [дан·с/кг] ;
[дан·с/кг] ; 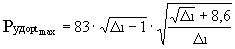 [дан·с/кг] ;
[дан·с/кг] ;
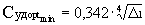 [кг/дан·ч] ;
[кг/дан·ч] ; 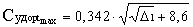 [кг/дан·ч] .
[кг/дан·ч] .
На рис.3 предельные Pудopt и Судopt
соответствуют: 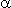 2 = 1 и
2 = 1 и 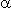 2
2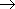
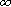 ,
соответственно.
,
соответственно.
Определенный интерес представляет ТРДК, у
которого отсутствует ограничение по подогреву 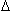 2 (так называемый
стехиометрический ТРДК).
2 (так называемый
стехиометрический ТРДК).
Величина подогрева  2 у
стехиометрического ТРДК зависит от
энергетических возможностей топлива, а также
степени сжатия рабочего тела е. Для
идеального ТРДК, работающего на керосине,
2 у
стехиометрического ТРДК зависит от
энергетических возможностей топлива, а также
степени сжатия рабочего тела е. Для
идеального ТРДК, работающего на керосине, 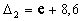 .
.
Суммарная работа циклов идеального
стехиометрического ТРДК, приходящаяся на 1кг
рабочего тела, определяется как
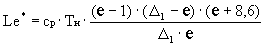
Оптимальная
степень сжатия е*opt
стехиометрического ТРДК определяется из условия
равенства производной функции Le*
по параметру е нулю:
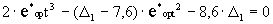 ,
,
На рис. 4 показано изменение
оптимальных степеней сжатия для
стехиометрического и оптимального (eopt = 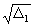 ) ТРДК.
) ТРДК.
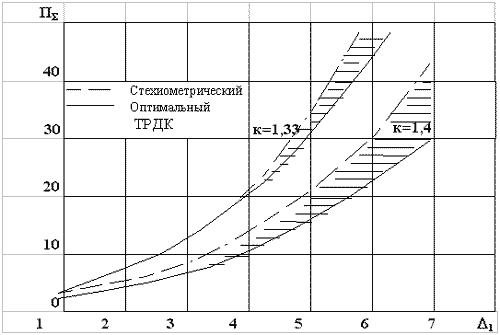
Рис.4
Видно, что стехиометрический ТРДК
имеет более высокие оптимальные степени сжатия
рабочего тела. Это связано с тем, что у ТРД,
имеющих ограничения по температуре газов,
увеличение степени сжатия рабочего тела
сопровождается уменьшением количества теплоты,
подводимой к двигателю, что является одной из
причин появленя П opt [3] .
Стехиометрический ТРДК имеет одно ограничение:
opt [3] .
Стехиометрический ТРДК имеет одно ограничение:  1, а оптимальный ТРДК два:
1, а оптимальный ТРДК два: 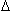 1 и
1 и  2. В связи с
этим процесс уменьшения количества теплоты,
связанный с увеличением П
2. В связи с
этим процесс уменьшения количества теплоты,
связанный с увеличением П , у
стехиометрического двигателя происходит более
медленно, так как
, у
стехиометрического двигателя происходит более
медленно, так как  2 в стехиометрическом ТРДК
увеличивается за счет сжатия воздуха, в то время
как в оптимальном ТРДК
2 в стехиометрическом ТРДК
увеличивается за счет сжатия воздуха, в то время
как в оптимальном ТРДК  2 остается постоянным.
2 остается постоянным.
На рис. 5 и 6 показаны диапазоны
изменения удельных параметров
стехиометрического и оптимального ТРДК в
условиях старта. Видно, что выигрыш от
использования стехиометрического двигателя
хотя и есть, но незначительный: удельный расход
топлива практически не меняется, а увеличение
удельной тяги находится в пределах 5%.
По-видимому, перспективы использования
стехиометрического двигателя связаны, главным
образом, с применением смешанных топлив, одно из
которых обладает повышенными по отношению к
керосину энергетическими возможностями. В этом
случае преимущества стехиометрического
двигателя становятся более очевидными.
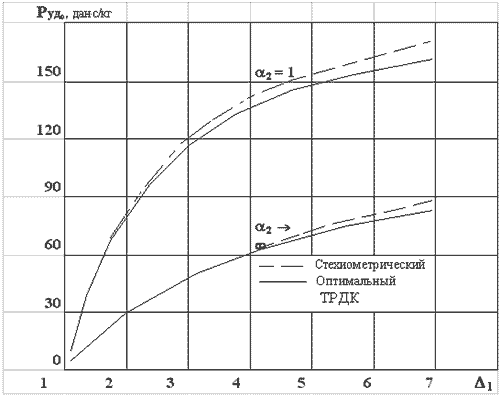
Рис.5
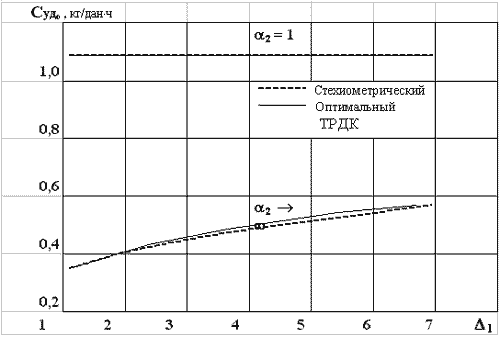
Рис.6
Анализ газодинамической схемы ТРДК (рис. 1) и
полученные результаты (рис. 3, 5, 6) показывают, что
двухкамерные ТРД обладают достаточно высоким
газодинамическим совершенством и способны
эффективно конкурировать с известными ТРД.
Реальный двухкамерный ТРД. В реальных ТРДК
все процессы, происходящие в его элементах,
сопровождаются потерями, а перепад давления на
турбине меньше степени повышения давления в
компрессоре. Кроме того, физические свойства
рабочего тела не остаются неизменными как в
связи с изменением температуры, так и за счет
отличия химического состава продуктов сгорания
и воздуха. Действительные циклы ТРДК,
изображенные в р-v координатах, показаны на рис. 7
(здесь Lrc Lrp - потери при сжатии и
расширении, соответственно).
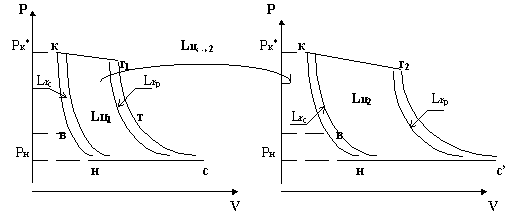
Рис.7
Точный учет всех условий протекания процессов
в воздушно-реактивных двигателях представляет
собой исключительно трудоемкий процесс. В связи
с этим в теории ВРД принят ряд упрощений,
позволяющих получать вполне приемлемые для
технических расчетов результаты. В частности,
считается неизменным количество рабочего тела,
теплоемкости воздуха и газа считаются
различными, но постоянными, суммарная степень
повышения давления П принимается
равной степени расширения газов, т.е. при
одинаковом начальном и конечном давлениях Рн и Рс*
одинаковыми принимаются максимальные давления Рк*
и Рг*. Наконец, КПД процессов сжатия в
воздухозаборнике и компрессоре и процессов
расширения в турбине и реактивном сопле
характеризуются осредненными величинами
принимается
равной степени расширения газов, т.е. при
одинаковом начальном и конечном давлениях Рн и Рс*
одинаковыми принимаются максимальные давления Рк*
и Рг*. Наконец, КПД процессов сжатия в
воздухозаборнике и компрессоре и процессов
расширения в турбине и реактивном сопле
характеризуются осредненными величинами 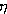 с и
с и 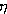 р,
соответственно.
р,
соответственно.
Работа действительного цикла Брайтона
определяется по методу, предложенному
академиком Стечкиным Б.С. [4] ,
 , (14)
, (14)
где 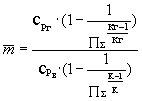 ,
,
П - суммарная
степень сжатия,
- суммарная
степень сжатия,
 - подогрев газа.
- подогрев газа.
Метод Стечкина Б.С. основан на принятых в теории
ВРД допущениях и позволяет достаточно
объективно учитывать потери, имеющие место в
действительном цикле Брайтона, а также различие
в физических свойствах воздуха и продуктов
сгорания.
В соответствии с (14) работа основного цикла,
приходящаяся на 1 кг рабочего тела, определяется
как
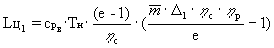 , (15)
, (15)
Работа дополнительного цикла, приходящаяся на 1
кг рабочего тела, определяется как
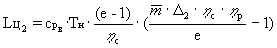 . (16)
. (16)
Суммарная работа циклов, приходящаяся на 1 кг
рабочего тела, в соответствии с (3) определяется
как
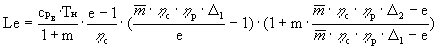 . (17)
. (17)
Коэффициент m, входящий в (17), определяется из
условия баланса работ турбины и компрессора:
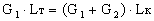 (18)
(18)
Работа турбины в соответствии с уравнением
Бернулли определяется как
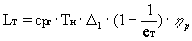 , (19)
, (19)
где 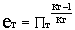 .
.
Работа компрессора в соответствии с уравнением
Бернулли определяется как
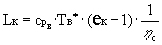 ,
,
где 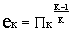 ,
,
или, учитывая, что Тв* = Тн·еv
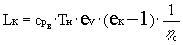 , (20)
, (20)
где 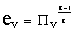 .
.
После подстановки (19) и (20) в (18) получаем
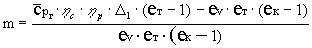 ,
,
где 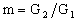 ,
,
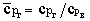 .
.
Умножив числитель и знаменатель полученного
уравнения на ек и
выполнив несложные преобразования, получаем
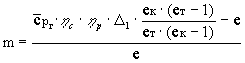 ,
,
где е = еv·eк.
Полагая 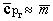 [3] и
вводя обозначение
[3] и
вводя обозначение 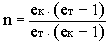 , окончательно получаем
, окончательно получаем
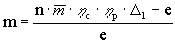 (21)
(21)
Коэффициент n, назовем его коэффициентом
двухкамерности, может быть представлен как
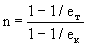 . (22)
. (22)
В соответствии с (22) коэффициент двухкамерности
является конструктивным параметром двигателя,
определяемым величинами Пк и Пт. На
рис.8 показаны зависимости коэффициента
двухкамерности от Пк и Пт.
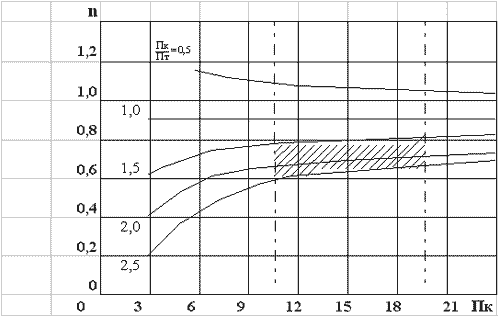
Рис.8
Видно, что для наиболее реальных соотношений
между Пк и Пт коэффициент двухкамерности
находится в пределах 0,6 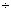 0,8
(заштрихованная область). Коэффициент
двухкамерности, как это следует из (21), оказывает
непосредственное влияние на распределение
рабочего тела между циклами двигателя.
Минимальное значение коэффициента
двухкамерности, при котором возможно
существование двигателя, определяется условием:
m = 0. Откуда
0,8
(заштрихованная область). Коэффициент
двухкамерности, как это следует из (21), оказывает
непосредственное влияние на распределение
рабочего тела между циклами двигателя.
Минимальное значение коэффициента
двухкамерности, при котором возможно
существование двигателя, определяется условием:
m = 0. Откуда
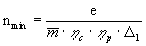 .
.
При n = nmin турбина не имеет
избыточной мощности, необходимой для сжатия
рабочего тела в дополнительном цикле. В этом
случае можно говорить о "вырождении"
двухкамерного ТРД. Таким образом, условием
существования ТРДК является неравенство
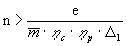 . (23)
. (23)
Подставляя (21) в (17) получаем
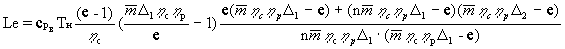 (24)
(24)
Выясним, какой характер имеет зависимость
суммарной работы реальных циклов ТРДК от П при заданном режиме полета и
постоянстве
при заданном режиме полета и
постоянстве  1,
1,  2,
2,
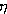 с,
с, 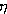 р. Le,
как видно из формулы (24), обращается в нуль при еmin
= 1 и еmax =
р. Le,
как видно из формулы (24), обращается в нуль при еmin
= 1 и еmax = 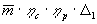 .
Значение П
.
Значение П opt определяется
из условия
opt определяется
из условия 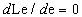 ,
т.е.
,
т.е.
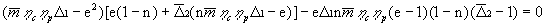 (25)
(25)
Анализ соотношения (25) показывает, что при n = 1
оптимальная суммарная степеннь сжатия ТРДК
соответствует оптимальной суммарной степени
сжатия ТРД:
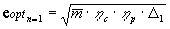 ;
; 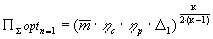 .
.
В остальных случаях наблюдается отличие в
значениях П opt. На рис. 9
показано изменение Leпр = Le/(cpв·Тн от П
opt. На рис. 9
показано изменение Leпр = Le/(cpв·Тн от П и n при
и n при  1 = 5.5 и
1 = 5.5 и  2 = 8
2 = 8
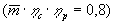 .
.
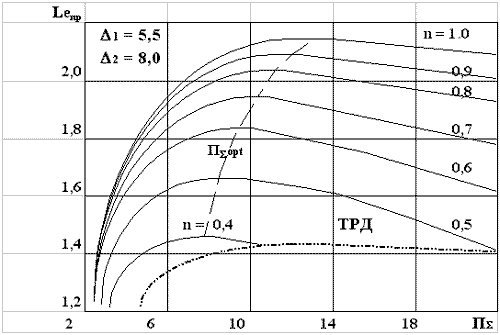
Рис.9
Видно, что П opt снижается
при уменьшении n от 1 до 0,4. Данное
обстоятельство объясняется различием работ
основного и дополнительного циклов, вызванное
различием подогревов
opt снижается
при уменьшении n от 1 до 0,4. Данное
обстоятельство объясняется различием работ
основного и дополнительного циклов, вызванное
различием подогревов  1 и
1 и  2. Дело в том, что суммарная
работа циклов, как это следует из (3), зависит как
от работы циклов, так и от доли каждого цикла в
суммарной работе (тем в большей степени, чем
больше разница в работах). Таким образом,
максимум суммарной работы будет достигнут тогда,
когда при максимальной доле цикла, имеющего
большую работу, работа каждого из циклов будет
также максимальной. Коэффициент n оказывает
непосредственное влияние (см. 21) на распределение
рабочего тела между циклами. Понижение n
уменьшает долю работы дополнительного цикла, что
при
2. Дело в том, что суммарная
работа циклов, как это следует из (3), зависит как
от работы циклов, так и от доли каждого цикла в
суммарной работе (тем в большей степени, чем
больше разница в работах). Таким образом,
максимум суммарной работы будет достигнут тогда,
когда при максимальной доле цикла, имеющего
большую работу, работа каждого из циклов будет
также максимальной. Коэффициент n оказывает
непосредственное влияние (см. 21) на распределение
рабочего тела между циклами. Понижение n
уменьшает долю работы дополнительного цикла, что
при  2 >
2 >  1
ведет к снижению суммарной работы. В этом случае
уменьшение П
1
ведет к снижению суммарной работы. В этом случае
уменьшение П позволяет повысить
долю работы дополнительного цикла и тем самым
добиться увеличения суммарной работы, но только
до тех пор, пока снижение работы циклов,
вызванное понижением П
позволяет повысить
долю работы дополнительного цикла и тем самым
добиться увеличения суммарной работы, но только
до тех пор, пока снижение работы циклов,
вызванное понижением П , не станет
определяющим. При n
, не станет
определяющим. При n 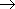 nmin (в
рассматриваемом примере ~ 0,4) доля
работы дополнительного цикла стремится к нулю,
что ведет к "вырождению" двухкамерного
двигателя.
nmin (в
рассматриваемом примере ~ 0,4) доля
работы дополнительного цикла стремится к нулю,
что ведет к "вырождению" двухкамерного
двигателя.
На рис. показана зависимость
относительной оптимальной степени сжатия 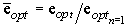 от n и
относительных подогревов
от n и
относительных подогревов 
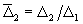 .
.
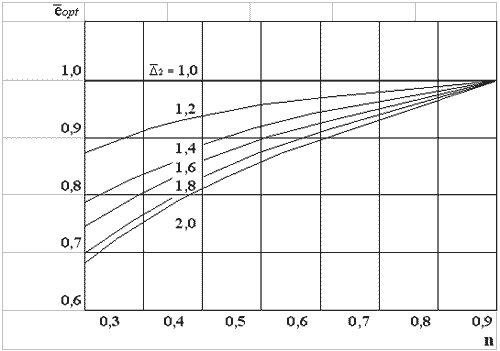
Рис.10
Влияние остальных параметров:  1,
1,
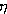 с,
с, 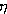 р,
входящих в соотношение (25), как показывает анализ,
несущественно. Таким образом, зависимость
р,
входящих в соотношение (25), как показывает анализ,
несущественно. Таким образом, зависимость 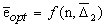 можно
рассматривать как универсальную по отношению к n
и
можно
рассматривать как универсальную по отношению к n
и 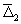 и
использовать при определении оптимальной
степени сжатия двухкамерных ТРД. В этом случае:
и
использовать при определении оптимальной
степени сжатия двухкамерных ТРД. В этом случае:
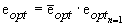 или
или 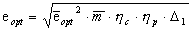 . (26)
. (26)
В формуле (26), по аналогии с ТРД, целесообразно
выполнить замену 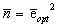 . Зависимость
. Зависимость 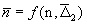 представлена на рис.11 и
аппроксимируется формулой
представлена на рис.11 и
аппроксимируется формулой
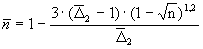 .
.
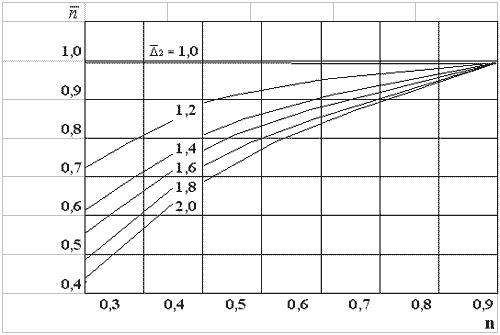
Рис.11
После замены 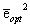 в (26) окончательно получаем
в (26) окончательно получаем
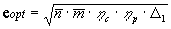 ;
; 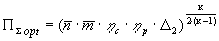 . (27)
. (27)
Выражение (27) показывает, что П opt
ТРДК ниже (на 5
opt
ТРДК ниже (на 5 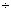 10 %) П
10 %) П opt ТРД, что объясняется причинами,
указанными выше. Повышение потерь в
действительных циклах приводит к снижению П
opt ТРД, что объясняется причинами,
указанными выше. Повышение потерь в
действительных циклах приводит к снижению П opt. Объясняется это, как и в
ТРД, тем, что при заданной величине подогрева с
ростом П
opt. Объясняется это, как и в
ТРД, тем, что при заданной величине подогрева с
ростом П уменьшается количество
подводимого с топливом тепла, а абсолютная
величина потерь сохраняется. При этом все
большая часть тепла тратится на компенсацию
указанных потерь. Если
уменьшается количество
подводимого с топливом тепла, а абсолютная
величина потерь сохраняется. При этом все
большая часть тепла тратится на компенсацию
указанных потерь. Если  1 увеличивается,
то П
1 увеличивается,
то П opt возрастает, так
как растет количество подводимого тепла, а доля
потерь, соответственно, уменьшается.
opt возрастает, так
как растет количество подводимого тепла, а доля
потерь, соответственно, уменьшается.
Следует отметить, что соотношение (27) получено
нами из условия постоянства температуры газа в
дополнительной камере сгорания. В том случае,
если в качестве ограничения выступает не
температура газа, а теплотворная способность
топлива (стехиометрический двигатель), то
подогрев  2 зависит от П
2 зависит от П и, соответственно, П
и, соответственно, П opt
будет несколько выше значения, определяемого
формулой (27). Однако, как показывают расчеты,
характер изменения суммарной работы циклов в
области максимальных значений весьма пологий
(рис. 9) и соотношение (27) можно считать практически
оптимальным и для этого случая, тем более, что с
целью уменьшения удельной массы двигателя
целесообразно несколько понижать П
opt
будет несколько выше значения, определяемого
формулой (27). Однако, как показывают расчеты,
характер изменения суммарной работы циклов в
области максимальных значений весьма пологий
(рис. 9) и соотношение (27) можно считать практически
оптимальным и для этого случая, тем более, что с
целью уменьшения удельной массы двигателя
целесообразно несколько понижать П по отношению к П
по отношению к П opt.
opt.
Эффективный КПД двигателя определяется как
отношение суммарной работы циклов к подведенной
теплоте: 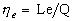 .
Количество теплоты Q, приходящееся на 1 кг
рабочего тела, определяется как
.
Количество теплоты Q, приходящееся на 1 кг
рабочего тела, определяется как
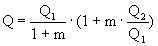 , (28)
, (28)
где Q1и Q2 - количество теплоты,
подведенное к 1 кг рабочего тела в основном и
дополнительном циклах, соответственно. Имея
ввиду, что 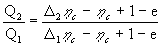 ,
после подстановки (21) в (28) получаем
,
после подстановки (21) в (28) получаем
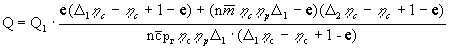 .
.
После подстановки Q и Le в формулу для
определения эффективного КПД получаем 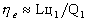 , т.е
, т.е 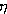 е
е 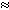
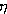 ц1.
ц1.
Основной цикл является действительным циклом
Брайтона, для которого закономерности изменения
КПД от П и величины потерь в
процессах расширения и сжатия известны [3] , а
экономическая степень повышения давления
определяется как
и величины потерь в
процессах расширения и сжатия известны [3] , а
экономическая степень повышения давления
определяется как
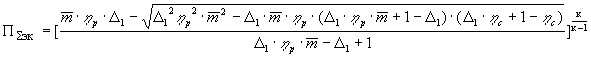
Оптимальные
значения П эк, найденные по
этой формуле, всегда больше, чем П
эк, найденные по
этой формуле, всегда больше, чем П opt
(см. 27). Это следует из анализа выражения КПД. При
увеличении П
opt
(см. 27). Это следует из анализа выражения КПД. При
увеличении П величина
подведенной теплоты Q непрерывно уменьшается
вследствие уменьшения разницы температур Тг1*-Тк*
(
величина
подведенной теплоты Q непрерывно уменьшается
вследствие уменьшения разницы температур Тг1*-Тк*
( 1 = const) и Тг2*-Тк*
(
1 = const) и Тг2*-Тк*
( 2 = const), а суммарная работа циклов
имеет максимум.
2 = const), а суммарная работа циклов
имеет максимум.
Выводы:
- Энергетические возможности двухкамерных ТРД
существенно выше энергетических возможностей
однокамерных ТРД (ТРДД). В идеальном случае
применение дополнительной камеры сгорания
увеличивает суммарную работу цикла по отношению
к однокамерному ТРД пропорционально отношению
подогревов в дополнительной и основной камерах
сгорания.
- Удельная тяга двухкамерного ТРД в
условиях взлета при использовании авиационного
керосина, теоретически, не превышает 150 дан·с/кг при удельном расходе топлива ~ 1,1 кг/дан·ч.
Минимальный удельный расход топлива,
теоретически, не может быть ниже 0,5 кг/дан·ч. Реальные удельные параметры
двигателя на 20
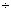 30% хуже
теоретических.
30% хуже
теоретических.
- Удельная тяга и удельный расход топлива в
двухкамерном ТРД изменяются практически
пропорционально.
- Характеристики действительного цикла
двухкамерного ТРД определяются коэффициентом
двухкамерности n = (1-1/eт)/(1-1/eк), который
характеризует степень преобразования
однокамерного двигателя в двухкамерный.
Расчетные значения коэффициента двухкамерности
находятся в пределах 0,6
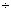 0,8.
0,8.
- Оптимальная суммарная степень повышения
давления в двухкамерном ТРД ниже оптимальной
суммарной степени повышения давления в
однокамерном ТРД на 5
 10 %.
Экономическая суммарная степень повышения
давления двухкамерного ТРД соответствует
экономической суммарной степени повышения
давления однокамерного ТРД.
10 %.
Экономическая суммарная степень повышения
давления двухкамерного ТРД соответствует
экономической суммарной степени повышения
давления однокамерного ТРД.
Список литературы
- Двухкамерный турбореактивный двигатель. Заявка
на изобретение ╧ 2000104340 от 21.02.2000, МПК F02 К 3/04 /
В.Л.Письменный /
- Абрамович Г.Н. Прикладная газовая
динамика. - М.: Наука, 1976. - 888 с.
- Теория и расчет воздушно-реактивных
двигателей. Под ред. С.М. Шляхтенко. - М.:
Машиностроение, 1978. - 568 с.
- Стечкин Б.С. Избранные труды. Теория
тепловых двигателей. - М.: Наука, 1977. - 410 с.
Сведения об авторе
Письменный Владимир Леонидович, доцент кафедры
испытаний авиационной техники филиала ⌠Взлет■
Московского государственного авиационного
института (технического университета), к.т.н.
 = 25 и степень двухконтурности m = 0,25.
Столь значительное снижение параметра m
объясняется повышением доли форсированных
режимов в общей наработке двигателей. В связи с
этим становится более выгодным понижать расходы
топлива на форсированных режимах, чем на
крейсерских, что возможно при значительном
снижении параметра m. В сложившейся ситуации
альтернативой двухконтурному форсированному
двигателю может стать двухкамерный
турбореактивный двигатель [1] (рис. 1), у которого
диапазон изменения удельных расходов топлива по
режимам существененно уже.
= 25 и степень двухконтурности m = 0,25.
Столь значительное снижение параметра m
объясняется повышением доли форсированных
режимов в общей наработке двигателей. В связи с
этим становится более выгодным понижать расходы
топлива на форсированных режимах, чем на
крейсерских, что возможно при значительном
снижении параметра m. В сложившейся ситуации
альтернативой двухконтурному форсированному
двигателю может стать двухкамерный
турбореактивный двигатель [1] (рис. 1), у которого
диапазон изменения удельных расходов топлива по
режимам существененно уже.

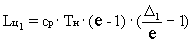 , (1)
, (1) 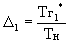 -
подогрев газа в основной камере сгорания,
-
подогрев газа в основной камере сгорания, - суммарная
степень сжатия.
- суммарная
степень сжатия.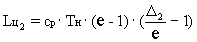 (2)
(2) 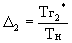 -
подогрев газа в дополнительной камере сгорания.
-
подогрев газа в дополнительной камере сгорания.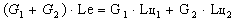 ,
,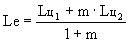 (3)
(3)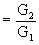 -
степень двухконтурности ТРДК.
-
степень двухконтурности ТРДК. , (4)
, (4)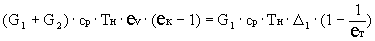 ,
,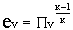 ;
; 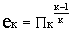 ;
; 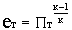 .
.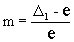 , (5)
, (5) 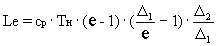 (6)
(6)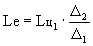
 2=const)
определяется также как в идеальном ТРД, а именно:
eopt =
2=const)
определяется также как в идеальном ТРД, а именно:
eopt = 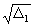 или
или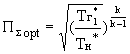 .
.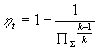 .
.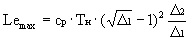 .
.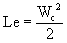 , откуда
, откуда 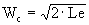 .
.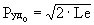 .
.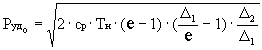 (7)
(7)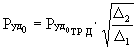 ,
,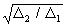 раз.
раз.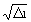 , определяем оптимальную
удельную тягу в условиях старта
, определяем оптимальную
удельную тягу в условиях старта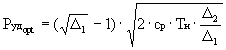 .
.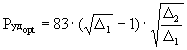 [дан·с/кг]. (8)
[дан·с/кг]. (8)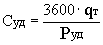 , (9)
, (9)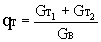 - суммарный относительный расход
топлива,
- суммарный относительный расход
топлива,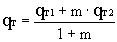
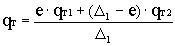 .
.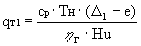 .
.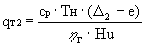 .
.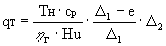 . (10)
. (10)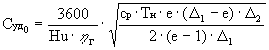 (11)
(11)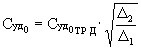 ,
,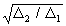 раз.
раз. 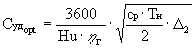 ,
, 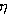 г = 0,98, соответственно:
г = 0,98, соответственно: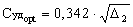 [кг/дан·ч] . (12)
[кг/дан·ч] . (12)
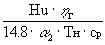 , (13)
, (13)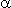 2 -
коэффициент избытка воздуха в дополнительной
камере сгорания.
2 -
коэффициент избытка воздуха в дополнительной
камере сгорания.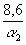 ,
,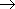
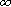 и
и
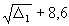 .
.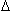 2max в (
2max в (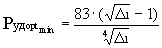 [дан·с/кг] ;
[дан·с/кг] ; 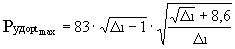 [дан·с/кг] ;
[дан·с/кг] ;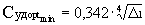 [кг/дан·ч] ;
[кг/дан·ч] ; 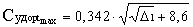 [кг/дан·ч] .
[кг/дан·ч] .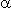 2
2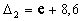 .
.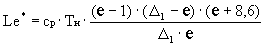
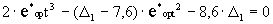 ,
,



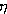 с и
с и  , (14)
, (14)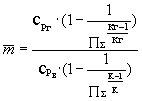 ,
,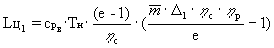 , (15)
, (15)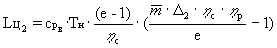 . (16)
. (16)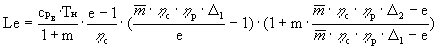 . (17)
. (17)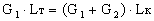 (18)
(18)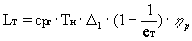 , (19)
, (19)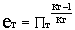 .
.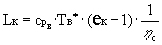 ,
,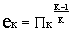 ,
,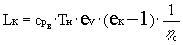 , (20)
, (20)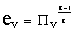 .
.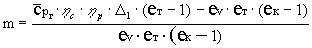 ,
,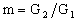 ,
,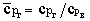 .
.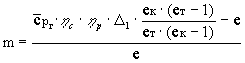 ,
, 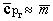 [
[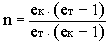 , окончательно получаем
, окончательно получаем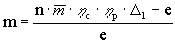 (21)
(21)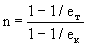 . (22)
. (22)
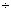 0,8
(заштрихованная область). Коэффициент
двухкамерности, как это следует из (
0,8
(заштрихованная область). Коэффициент
двухкамерности, как это следует из (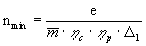 .
.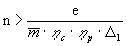 . (23)
. (23) 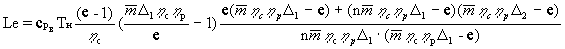 (24)
(24)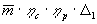 .
Значение П
.
Значение П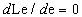 ,
т.е.
,
т.е. 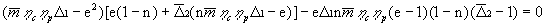 (25)
(25)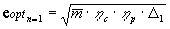 ;
; 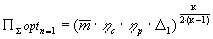 .
.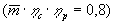 .
.
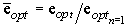 от n и
относительных подогревов
от n и
относительных подогревов 
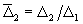 .
.
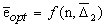 можно
рассматривать как универсальную по отношению к n
и
можно
рассматривать как универсальную по отношению к n
и 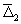 и
использовать при определении оптимальной
степени сжатия двухкамерных ТРД. В этом случае:
и
использовать при определении оптимальной
степени сжатия двухкамерных ТРД. В этом случае: 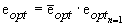 или
или 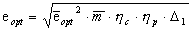 . (26)
. (26)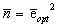 . Зависимость
. Зависимость 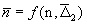 представлена на рис.11 и
аппроксимируется формулой
представлена на рис.11 и
аппроксимируется формулой 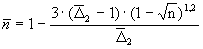 .
. 
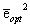 в (
в (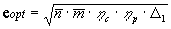 ;
; 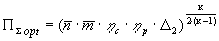 . (27)
. (27)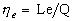 .
Количество теплоты Q, приходящееся на 1 кг
рабочего тела, определяется как
.
Количество теплоты Q, приходящееся на 1 кг
рабочего тела, определяется как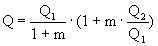 , (28)
, (28)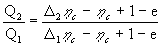 ,
после подстановки (
,
после подстановки (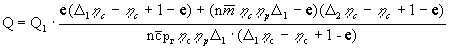 .
. 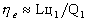 , т.е
, т.е