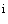 } (1
} (1 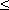 i
i
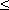 m). Требуется смоделировать
нейронную сеть, которая восстанавливает
искаженный эталонный образ вектора x.
m). Требуется смоделировать
нейронную сеть, которая восстанавливает
искаженный эталонный образ вектора x.УДК 004.032.26(063)
Использование аппарата нейронных сетей для решения задачи восстановления графических изображений
Е. М. Будкина
Рассматривается применение функции сигмоидного типа в качестве функции активации нейронной сети Хопфилда. Проводится аналогия между функционированием рассматриваемой сети и гомогенным нечетким множеством типа k. Показана эффективность применения сети Хопфилда с функцией гиперболического тангенса для восстановления сильно искаженных изображений.
В последние годы наблюдается повышенный интерес к искусственном нейронным сетям (НС), они находят успешное применение в самых различных областях - бизнесе, медицине, физике, технике.
Как правило, НС используется для решения задач, в которых неизвестен точный вид связей между исходными данными и результатом, но накоплено достаточное число экспериментальных данных (к таким задачам относится в частности задача восстановления графических образов).
Качество классификации изображений в значительной мере зависит от степени их искажения, поэтому задача восстановления графических образов является актуальной. Поэтому исходное изображение должно пройти предобработку восстановлением.
Постановка задачи
Пусть задан набор из m эталонов изображений -
n-мерных векторов {x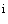 } (1
} (1 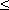 i
i
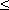 m). Требуется смоделировать
нейронную сеть, которая восстанавливает
искаженный эталонный образ вектора x.
m). Требуется смоделировать
нейронную сеть, которая восстанавливает
искаженный эталонный образ вектора x.
Классическая сеть Хопфилда
Для решения поставленной задачи рассматривается сеть ассоциативной памяти - сеть Хопфилда. Такая сеть позволяет соотносить входное изображение с уже знакомыми ей графическими образами и дополнять его до полного вида, а также отфильтровывать из входного изображения недостоверную информацию [1] .
Входные и выходные сигналы сети биполярные: (+1 и -1). Для задачи восстановления графических образов входной сигнал равен 1, если пиксел черного цвета и равен -1 если пиксел белого цвета.
Нейрон получает на вход вектор сигналов х, вычисляет его скалярное произведение на вектор весовых коэффициентов s и преобразует его активационной функцией f (рис. 1) [1, 2, 3]. Сеть Хопфилда имеет жесткие пороговые активационные функции, например sign:
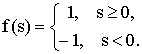 (1)
(1)
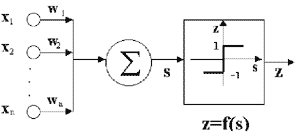
Структурная схема функционирования
одного нейрона.
Рис. 1.
Сеть функционирует циклически (рис. 2), осуществляя преобразование:
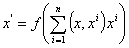 , (2)
, (2)
где скалярное произведение (x,x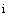 ) - вес i-го эталона.
) - вес i-го эталона.
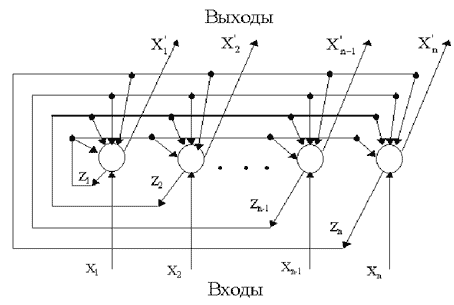
Структурная схема функционирования
сети Хопфилда.
Рис. 2.
Правило формирования весовых коэффициентов следующее:
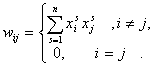 (3)
(3)
То есть коэффициенты вычисляются, как сумма произведений векторов входа по соответствующим индексам. Матрица весовых коэффициентов W симметрична относительно нулевой главной диагонали.
Функционирование сети происходит рекуррентно:
z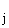 (t + 1) = f
(t + 1) = f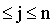 , (4)
, (4)
при начальном условии: z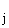 (0) = x
(0) = x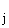 , 1
, 1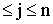 .
.
Процесс распознавания завершает свою работу после того, как выходные сигналы нейронов перестают изменяться, то есть значение выхода на некотором шаге T равно значению выхода на предыдущем шаге (T-1):
z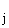 (T) = z
(T) = z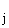 (T - 1), 1
(T - 1), 1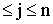 . (5)
. (5)
Таким образом, полученный выходной сигнал сети имеет вид:
x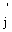 = z
= z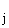 (T), 1
(T), 1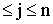 . (6)
. (6)
Сеть Хопфилда имеет существенные недостатки:
1) небольшая емкость, то есть число образов, которое сеть может запомнить не превышает 0,15*n от размерности n входного вектора;
2) запоминаемые образы не должны быть сильно скоррелированы.
Для устранения этих недостатков в настоящей статье для решения поставленной задачи рассматриваются различные преобразования классической сети Хопфилда.
Ортогональная сеть Хопфилда
Степень скоррелированности образов определяется отношением:
K=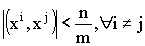 (7)
(7)
Сеть Хопфилда с ортогональным преобразованием позволяет восстанавливать сильно скоррелированные образы и выполнять следующие преобразования [1] :
x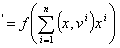 , (8)
, (8)
где v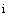 - векторы дуального множества,
которые равны:
- векторы дуального множества,
которые равны:
v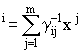 , (9)
, (9)
где 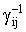 - элемент обратной матрицы Грама Г
- элемент обратной матрицы Грама Г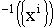 :
: 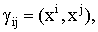 ij- ый
элемент матрицы Грама равен скалярному
произведению i-го эталона на j-ый.
ij- ый
элемент матрицы Грама равен скалярному
произведению i-го эталона на j-ый.
Для работы ортогональной сети Хопфилда
необходимо хранить эталоны и обратную матрицу
Грама 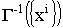 .
.
Ортогональное преобразование снижает зависимость надежности работы сети от степени скоррелированности образов, а также увеличивает емкость сети.
Автокорреляторная сеть Хопфилда
Применение автокорреляторов позволяет обрабатывать визуальные образы, отличающиеся только положением в рамке. Для этого исходное изображение преобразуется в вектор инвариантов, не изменяющийся при сдвиге. Простейший набор инвариантов дают автокорреляторы, которые являются скалярным произведением образа на сдвинутый образ и рассматриваются как функции вектора сдвига.
Автокорреляторная сеть имеет вид:
x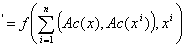 (10)
(10)
Вычисление сдвигового автокоррелятора для
черно-белых изображений проводится следующим
образом. Пусть дан двумерный образ d размером p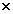 q=n. Обозначим
точки образа как d
q=n. Обозначим
точки образа как d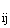 . Элементами
автокоррелятора Ac(d) будут
величины:
. Элементами
автокоррелятора Ac(d) будут
величины: 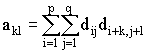 .
.
Автокорреляторное преобразование сети позволяет обрабатывать различные образы, отличающиеся только положением в рамке [1] .
Нечеткая сеть Хопфилда с сигмоидной функцией активации
Использование пороговой функции в качестве активационной функции сети Хопфилда значительно ограничивает возможности сети. Качество работы такой сети зависит от степени искажения исходного изображения. Для повышения надежности восстановления в настоящей работе предлагается метод с использованием в качестве функции активации функции гиперболического тангенса:
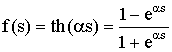 (11)
(11)
Функция гиперболического тангенса (рис. 3) с
большим значением характеристики 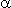 приближается по внешнему виду к пороговой
функции (рис. 1).
приближается по внешнему виду к пороговой
функции (рис. 1).
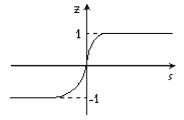
График функции гиперболического
тангенса.
Рис. 3.
Применение такой активационной функции позволяет увеличить способность сети запоминать и точно воспроизводить сильно искаженные эталоны.
Таким образом, преобразованная сеть Хопфилда будет иметь вид:
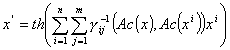 . (12)
. (12)
Утверждение. НС Хопфилда с функцией гиперболического тангенса реализует гомогенное n√мерное нечеткое множество (НМ) типа k, где n √ число элементов сети Хопфилда, k √ число тактов функционирования сети.
Доказательство.
1. Введем понятие НМ A для
сети Хопфилда. Каждый нейрон НС соответствует
одному пикселу изображения, который может иметь
только одно из двух значений цветов: черный или
белый. Сеть с функцией активации (1) однозначно
определяет цвет каждого пиксела. Сеть с функцией
активации (11) каждому пикселу ставит в
соответствие число из интервала [-1, 1], которое
можно рассматривать как степень близости к
черному или белому цвету. Таким образом для
каждого элемента x  X один нейрон
сети сопоставляет нечеткое множество А ={(x,
X один нейрон
сети сопоставляет нечеткое множество А ={(x, 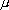 A(x))}, где
A(x))}, где 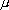 A
√ число, характеризующее степень принадлежности
элемента x множеству A, осуществляя отображение
A
√ число, характеризующее степень принадлежности
элемента x множеству A, осуществляя отображение 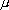 A:X
A:X 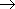 [-1, 1]. По
определению [4] введенное множество является НМ
типа 1.
[-1, 1]. По
определению [4] введенное множество является НМ
типа 1.
2. Так как НС состоит из n
нейронов, то каждый элемент x  X характеризуется вектором значений
принадлежности (
X характеризуется вектором значений
принадлежности (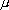 1(x),
1(x), 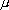 2(x),┘,
2(x),┘, 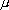 n(x)), где
n(x)), где 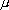 i(x) √значение функции принадлежности i-го нейрона, (i=1,2,┘,n).
Таким образом, строится функция, отображение
которой представляется в виде:
i(x) √значение функции принадлежности i-го нейрона, (i=1,2,┘,n).
Таким образом, строится функция, отображение
которой представляется в виде:
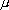 :X
:X 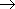 S1
S1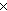 S1
S1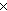 ┘
┘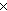 Sn , (13)
Sn , (13)
где Si (i=1,2,┘,n) √ ограниченные линейно упорядоченные множества на интервале [-1, 1].
По признаку однородности области значений функций принадлежности, построенное НМ является гомогенным n-мерным и имеет вид:
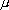 :X
:X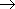 [-1,1]n. (14)
[-1,1]n. (14)
3. Процесс функционирования сети (4) в обозначениях НМ имеет вид:
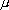 t+1(X) =
t+1(X) = 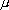 (
(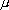 t(X)), (15)
t(X)), (15)
при начальном условии 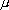 0(X)=X.
0(X)=X.
Таким образом на каждом шаге t (1 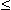 t
t 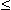 k) функционирования
НС реализуется НМ типа t [4] :
k) функционирования
НС реализуется НМ типа t [4] :
|
┘,
| (16) |
Утверждение доказано.
Численный эксперимент
Апробация метода с использованием функции
гиперболического тангенса, осуществлялась с
помощью численного эксперимента, который
заключался в восстановлении отпечатков пальцев.
В качестве исходных данных взяты растровые
черно-белые изображения отпечатков пальцев
размером 40х50 пикселей. Таким образом входной
вектор 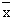 = {x1, x2,┘,xm} и выходной вектор
= {x1, x2,┘,xm} и выходной вектор 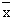 ' =
{x'1, x'2,┘,x'm} имеют
размерность m=2000.
' =
{x'1, x'2,┘,x'm} имеют
размерность m=2000.
Исходными данными для формирования весовых коэффициентов сети являются векторы-образцы, содержащиеся в базе эталонов. При восстановлении изображения, сеть осуществляет преобразование входного вектора x так, чтобы выходной вектор x▓ максимально соответствовал эталону, который рассматривается как правильный ответ.
Сравнительная характеристика работы классической и преобразованной сети Хопфилда приведена табл. 1.
Сравнительный анализ полученных результатов позволяет сделать следующие выводы: качество восстановления изображения НС с пороговой функцией в значительной мере зависит от степени искажения изображения, такая сеть практически не восстанавливает значительно смещенные от мнимого центра образы, имеющие частичную потерю фрагментов. НС с функцией гиперболического тангенса не восстанавливает только те изображения, потеря фрагментов которых составляет более 85% при несмещенном изображении и более 75% при смещенном от мнимого центра изображения.
Таблица 1
Сравнение преобразованных сетей Хопфилда
| Модель НС | Качество распознавания (в %) | ||
| потеря информации 20% | потеря информации от 20% до 50% | потеря информации более 50% | |
| Преобразованная сеть Хопфилда с пороговой функцией активации sign | 100 | 73 | 51 |
| Преобразованная сеть Хопфилда с сигмоидной функцией активации th | 100 | 100 | 97 |
В табл. 2 приведены результаты восстановления искаженных отпечатков пальцев преобразованной сетью Хопфилда с функцией гиперболического тангенса. Приведены примеры сдвинутых отпечатков, отпечатков с частичной потерей фрагментов.
Таблица 2.
Примеры восстановления отпечатков пальцев.

Дальнейшие исследования предполагают рассмотреть восстановление полутоновых и цветных изображений, обработку аэрокосмических изображений (сжатие, восстановление, сегментация, констатирование и обработка текстур), поиск и восстановление на изображении объектов заданной формы, обработка серии или потоков изображений.
Выводы
В настоящей статье для задачи восстановления графических изображений предлагается использовать нейронную сеть Хопфилда с функцией активации √ гиперболический тангенс. Анализируется связь предложенной НС с теорией нечетких множеств. Результаты, полученные при реализации численного эксперимента, показали эффективность применения НС Хопфилда с функцией гиперболического тангенса для восстановления сильно искаженных изображений.
Список литературы
Сведения об авторе
Будкина Елена Михайловна, старший преподаватель кафедры математического и программного обеспечения информационных систем комплексов и сетей филиала ⌠Восход■ Московского государственного авиационного института (технического университета), аспирантка кафедры дифференциальных уравнений Московского государственного авиационного института (технического университета).
E-mail: lenok@baikonur.ru