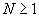 )
в алфавите
)
в алфавите 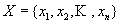 (
(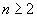 ). Для описания алгоритма упорядочим
как-либо буквы из алфавита X и для упрощения обозначений
положим, что X={1,2,┘,n}.
). Для описания алгоритма упорядочим
как-либо буквы из алфавита X и для упрощения обозначений
положим, что X={1,2,┘,n}.УДК 681.3
Статистический алгоритм сжатия информации
С.В. Лобанов
В данной статье представлено описание алгоритма кодирования перестановок с повторе-ниями, являющегося статистическим алгоритмом сжатия информации. Рассматриваются два варианта метода: двухпроходный, требующий априорно знания статистики кодируемой после-довательности, и однопроходный, формирующий статистику в процессе работы. Показывается асимптотическая оптимальность алгоритма при увеличении длины последовательности. Приво-дится зависимость времени кодирования от длины сжимаемой последовательности. Сообщает-ся о практических результатах моделирования алгоритма на ЭВМ.
Описание алгоритма
При удалении избыточности из сообщения, порождаемого дискретным источником информации, различают случаи, когда априорно известна или неизвестна его статистика. Рассматриваемый в данной статье алгоритм нумерационного кодирования (АНК) можно одинаково эффективно использовать в обоих случаях, т.к. имеются две модификации алгоритма, использующих одну концептуальную модель [1, 2, 3]. Первая модификация алгоритма требует перед кодированием наличия статистики сжимаемого блока данных, вторая ее не требует, а формирует по мере поступления элементов последовательности. В любом случае процедура кодирования состоит в том, что любой последовательности некоторой длины букв дискретного источника информации ставится в соответствие кодовое слово, состоящее из двух частей: в одной указывается состав последовательности √ код состава (КС), в другой √ номер последовательности с данным составом √ код расположения (КР) [3] . АНК относится к группе алгоритмов без потери информации, т.е. является универсальным.
При нумерационном кодировании
дискретный источник информации S задается как произвольное
подмножество множества слов длины N (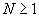 )
в алфавите
)
в алфавите 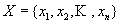 (
(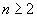 ). Для описания алгоритма упорядочим
как-либо буквы из алфавита X и для упрощения обозначений
положим, что X={1,2,┘,n}.
). Для описания алгоритма упорядочим
как-либо буквы из алфавита X и для упрощения обозначений
положим, что X={1,2,┘,n}.
Любую последовательность букв дискретного источника информации
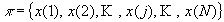 ,
,
можно представить в виде перестановки
составляющих ее элементов. Здесь x(j) √ элемент с порядковым номеромx
(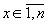 ), стоящий на j-ой
(
), стоящий на j-ой
(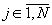 ) позиции перестановки. Если в
перестановке
) позиции перестановки. Если в
перестановке 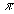 содержится
содержится 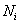 элементов с номером i (
элементов с номером i (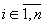 ), то, очевидно,
выполняется следующее соотношение
), то, очевидно,
выполняется следующее соотношение
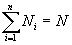 , (1)
, (1)
где N - количество элементов в последовательности (длина последовательности).
Общее число перестановок заданного
состава 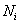 , т.е. мощность множества S, определяется известным в
комбинаторике выражением для числа перестановок
с повторениями
, т.е. мощность множества S, определяется известным в
комбинаторике выражением для числа перестановок
с повторениями
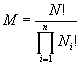 (2)
(2)
Несложно показать, что мощность
источника S можно
выразить через вероятности 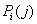 появления
символов алфавита на соответствующих позициях
перестановки
появления
символов алфавита на соответствующих позициях
перестановки 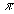 следующим образом
следующим образом
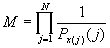
если определить, что 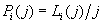 или
или 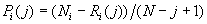 ,
где
,
где 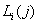 ,
, 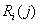 -
количество символов с порядковым номером i среди первых j и (
-
количество символов с порядковым номером i среди первых j и (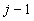 ) элементов
последовательности соответственно.
) элементов
последовательности соответственно.
Следует отметить, что, т.к. приход
одного из n символов
алфавита является обязательным событием, то на
каждом шаге кодирования они образуют полную
группу несовместных событий с вероятностями 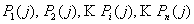 .
Следовательно, на каждой j-ой
позиции
.
Следовательно, на каждой j-ой
позиции 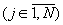 перестановки
перестановки 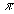 соблюдается
равенство
соблюдается
равенство

Таким образом, математической моделью
последовательности при кодировании по АНК
является перестановка элементов 1,2,┘,n с повторениями 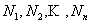 раз
соответственно. Это означает, что каждой
перестановке из некоторого множества S надо поставить в соответствие ее
номер из натурального ряда чисел
раз
соответственно. Это означает, что каждой
перестановке из некоторого множества S надо поставить в соответствие ее
номер из натурального ряда чисел 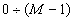 , где M -
мощность множества S.
, где M -
мощность множества S.
Вообще при фиксированной величине n алфавита дискретного источника
информации и длине последовательности 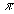 равной N общее число групп
перестановок с различным составом определяется
по формуле комбинаторики для числа сочетаний с
повторениями
равной N общее число групп
перестановок с различным составом определяется
по формуле комбинаторики для числа сочетаний с
повторениями
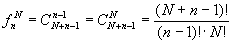
В основу алгоритма нумерации
перестановок заложен принцип цепного разбиения
множества перестановок на подмножества по
каждой из позиций перестановки. Процедура
разбиения множества перестановок на
подмножества, позволяющая установить
взаимно-однозначное соответствие между любой
перестановкой 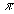 из множества S и ее номером из натурального ряда
чисел
из множества S и ее номером из натурального ряда
чисел  , представлена на рис.1, где имеют
место следующие обозначения:
, представлена на рис.1, где имеют
место следующие обозначения:
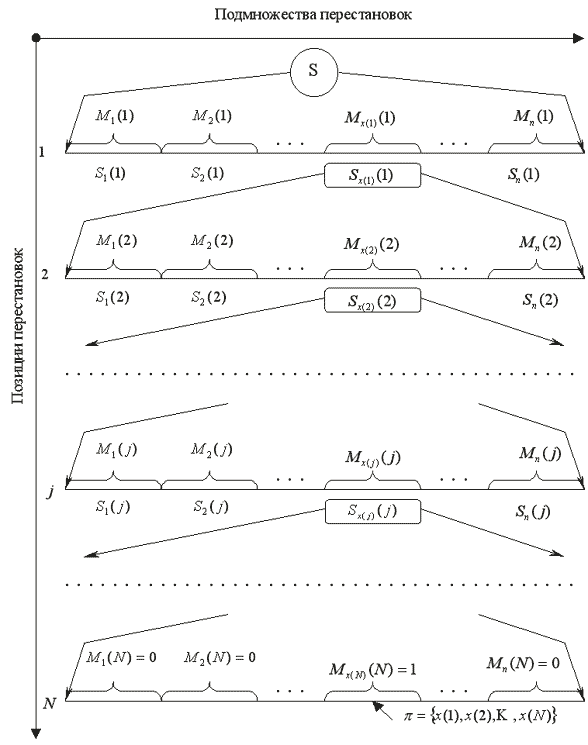
Рис. 1. Процедура разбиения множества перестановок на подмножества.
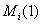 - мощность i-го
подмножества
- мощность i-го
подмножества 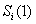 , полученного при
разбиении исходного множества S по первой позиции перестановки;
, полученного при
разбиении исходного множества S по первой позиции перестановки;
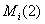 - мощность i-го
подмножества
- мощность i-го
подмножества 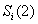 , полученного при
разбиении подмножества
, полученного при
разбиении подмножества 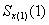 по второй
позиции перестановки;
по второй
позиции перестановки;
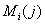 - мощность i-го
подмножества
- мощность i-го
подмножества 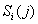 , полученного при
разбиении подмножества
, полученного при
разбиении подмножества 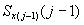 по j-ой позиции перестановки.
по j-ой позиции перестановки.
Таким образом, N
строк разбиения соответствуют N позициям перестановки 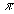 ,
причем каждая строка состоит из n подмножеств.
,
причем каждая строка состоит из n подмножеств.
Для установления взаимно-однозначного
соответствия между любой перестановкой 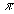 из множества S
и ее номером K(
из множества S
и ее номером K(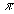 ) из натурального
ряда
) из натурального
ряда 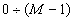 достаточно в качестве номера
перестановки взять сумму мощностей всех
подмножеств, предшествующих выделенным в
разбиении по каждой из позиции [4]
достаточно в качестве номера
перестановки взять сумму мощностей всех
подмножеств, предшествующих выделенным в
разбиении по каждой из позиции [4]
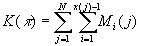 (3)
(3)
Мощность 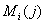 подмножества
перестановок
подмножества
перестановок 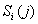 равна произведению
мощности
равна произведению
мощности 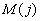 источника S
на j-ом шаге кодирования
на вероятность появления
источника S
на j-ом шаге кодирования
на вероятность появления 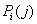 на j-ой позиции последовательности
элемента c i-ым порядковым
номером
на j-ой позиции последовательности
элемента c i-ым порядковым
номером
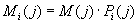 (4)
(4)
Вообще дальше возможны два пути
трактовки того, что из себя представляют
подмножества 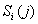 . В зависимости от этого
получаются разные выражения, определяющие
. В зависимости от этого
получаются разные выражения, определяющие 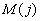 ,
, 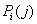 и, как
следствие,
и, как
следствие, 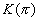 .
.
Первый вариант состоит в следующем. В
подмножество 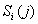 входят перестановки, у
которых первые
входят перестановки, у
которых первые 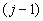 элементов совпадают с
первыми
элементов совпадают с
первыми 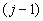 элементами перестановки
элементами перестановки 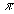 ,
а на j-ой позиции стоит
элемент
,
а на j-ой позиции стоит
элемент 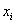
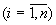 .
Следовательно, поскольку первые
.
Следовательно, поскольку первые 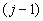 элементов
перестановок подмножества
элементов
перестановок подмножества 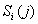 зафиксированны, то вероятность появления на j-ой позиции перестановки
зафиксированны, то вероятность появления на j-ой позиции перестановки 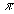 элемента
элемента 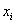 определяется их количеством
определяется их количеством 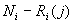 среди всех
среди всех 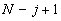 оставшихся элементов,
т. е.
оставшихся элементов,
т. е.
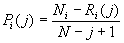 (5)
(5)
где 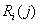 - количество элементов
с порядковым номером i
среди первых
- количество элементов
с порядковым номером i
среди первых 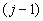 элементов
перестановки
элементов
перестановки 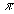 . Мощность
. Мощность 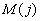 источника S на j-ой позиции перестановки можно
определить следующим образом
источника S на j-ой позиции перестановки можно
определить следующим образом
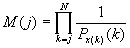
Подставив в 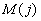 выражение для
выражение для 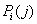 из (5) получим формулу
из (5) получим формулу
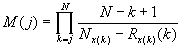 ,
,
которой эквивалентна следующая форма записи
 (6)
(6)
в силу очевидного соотношения
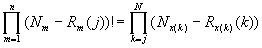
Вообще выражение (2) является частным случаем выражения (6) при j=1. Таким образом, подставляя в (4) выражения (5) и (6), получаем
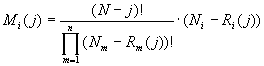 (7)
(7)
В итоге подстановкой 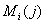 из (7) в (3)
формируем окончательно соотношение для
определения номера перестановки
из (7) в (3)
формируем окончательно соотношение для
определения номера перестановки 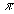
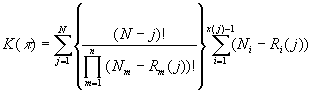 (8)
(8)
Такая схема кодирования обладает следующим недостатком: перед сжатием по выражению (8) необходимо знать априорно статистику последовательности, т.е. ее КС. Поэтому алгоритм является двухпроходным.
Возможен другой вариант АНК, который
лишен этого недостатка, т.к. он формирует КС по
мере поступления символов из входного потока,
если определить подмножество 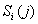 исходя из других соображений. Пусть в
подмножество
исходя из других соображений. Пусть в
подмножество 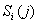 входят перестановки, у
которых последние
входят перестановки, у
которых последние 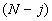 элементов
зафиксированы, а на j-ой
позиции стоит элемент
элементов
зафиксированы, а на j-ой
позиции стоит элемент 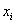
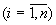 . Тогда вероятность
появления на j-ой позиции
последовательности i-го
элемента алфавита равна
. Тогда вероятность
появления на j-ой позиции
последовательности i-го
элемента алфавита равна
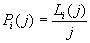 (9)
(9)
где 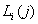 - количество элементов
- количество элементов 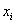 среди первых j элементов
перестановки
среди первых j элементов
перестановки 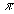 . Мощность
. Мощность 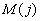 источника S на j-ой позиции перестановки можно
определить следующим образом
источника S на j-ой позиции перестановки можно
определить следующим образом
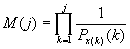
Подставляя в предыдущее выражение
значение 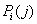 из (9), получим мощность множества S
на j-ом
шаге кодирования
из (9), получим мощность множества S
на j-ом
шаге кодирования
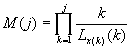
Используя следующее тождество, справедливое для любой последовательности,
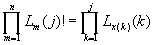 ,
,
выражение для 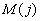 запишем
несколько иным образом
запишем
несколько иным образом
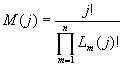 (10)
(10)
Следует обратить внимание, что
выражение (2) является частным случаем
соотношения (10) при j=N. Тогда
мощность множества 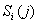 , определяемая по
формуле (4), с учетом (9) и (10) будет следующей
, определяемая по
формуле (4), с учетом (9) и (10) будет следующей
 (11)
(11)
В результате, подставляя (11) в (3), окончательно получаем
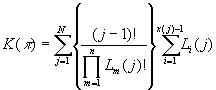 (12)
(12)
Такая схема кодирования обладает следующим недостатком: восстановленная последовательность будет иметь порядок расположения элементов, обратный по отношению к исходной. По данному варианту алгоритма написана программа на языке ассемблера для компьютеров типа IBM PC/AT, которая позволяет менять размер КР от 4 байт до 64 кБайт.
При реализации алгоритмов сжатия на ЭВМ очень удобно иметь рекуррентную форму записи процедуры кодирования и декодирования. Обе разновидности нумерационного кодирования имеют рекуррентную форму записи, которая, например, приведена в [1] .
Процедура восстановления для двух
приведенных выше вариантов нумерационного
кодирования одинакова [3] . Она требует наличия
перед декодированием наряду с 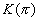 , также КС
последовательности. Следовательно, его
необходимо передавать по каналу связи (сохранять
на носителе информации) наряду с КР, что вводит
дополнительную избыточность и уменьшает
коэффициент сжатия алгоритма.
, также КС
последовательности. Следовательно, его
необходимо передавать по каналу связи (сохранять
на носителе информации) наряду с КР, что вводит
дополнительную избыточность и уменьшает
коэффициент сжатия алгоритма.
Асимптотическая оптимальность нумерационного кодирования
Покажем, что нумерационное кодирование асимптотически оптимально при увеличении длины последовательности N. Очевидно, что код будет оптимальным, если сумма удельных длин КС и КР, приходящихся на один входной элемент, будет всего лишь на малую величину больше, чем энтропия H дискретного источника информации без памяти.
Исследуем сначала на оптимальность КР. КР является номером перестановки данного состава, общее число которых определяется формулой (2). Удельная длина КР, приходящаяся на один элемент последовательности (далее и везде, если не оговорено особо, подразумевается двоичный логарифм)
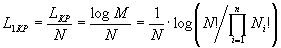 (13)
(13)
Воспользовавшись формулой Стирлинга вида
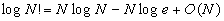 ,
,
где
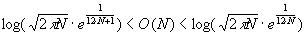 ,
,
преобразуем выражение (13) к следующему виду
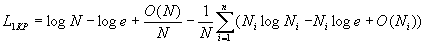
Используя равенство (1) и проведя дополнительные преобразования, предыдущее выражение можем записать следующим образом
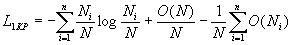 (14)
(14)
Можно показать, что
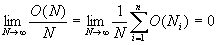
Следовательно, 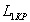 при
при 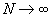 сходится по вероятности к энтропии источника
сходится по вероятности к энтропии источника
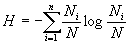
Значит КР является оптимальным.
Теперь рассмотрим оптимальность КС.
При любом способе кодирования существует
некоторый максимальный размер 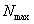 последовательности, при котором происходит
заполнение разрядной сетки КС в силу ее
конечности. Пусть КС формируется простейшим
способом, а именно: кодирование состава сводится
к подсчету букв каждого типа в общем случае на n счетчиках разрядности
последовательности, при котором происходит
заполнение разрядной сетки КС в силу ее
конечности. Пусть КС формируется простейшим
способом, а именно: кодирование состава сводится
к подсчету букв каждого типа в общем случае на n счетчиках разрядности 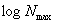 каждый. Такой способ формирования КС наиболее
простой, но не самый оптимальный. Следовательно
относительная длина КС, приходящаяся на один
элемент входной последовательности
каждый. Такой способ формирования КС наиболее
простой, но не самый оптимальный. Следовательно
относительная длина КС, приходящаяся на один
элемент входной последовательности
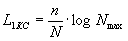 (15)
(15)
Принимая во внимание, что 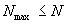 и n<<
и n<<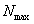 , получим
, получим
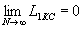
Таким образом, описанный выше способ нумерационного кодирования является асимптотически оптимальным, т.к. удельная длина кода
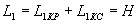
при 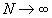 .
.
Зависимость времени кодирования от длины последовательности
Время, затраченное на кодирование по алгоритму АНК последовательности длиной N, равно
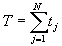 , (16)
, (16)
где 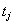 - время обработки
элемента x(j), стоящего
на j-ой позиции
перестановки
- время обработки
элемента x(j), стоящего
на j-ой позиции
перестановки 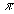 . Время обработки
элемента x(j) на каждом
отдельном шаге jпрямо
пропорционально длине КР на этом шаге
. Время обработки
элемента x(j) на каждом
отдельном шаге jпрямо
пропорционально длине КР на этом шаге
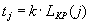 (17)
(17)
Коэффициент пропорциональности k имеет размерность сек/бит. Он показывает, сколько времени затрачивается на обработку одного бита КР. Длина КР на шаге j определяется как
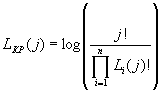
Используя (14) можем записать
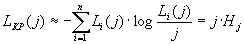
Здесь
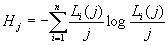
энтропия источника информации на j-й позиции последовательности. Примем, что энтропия источника не меняется от шага к шагу, т.е. постоянна и равна H. Тогда относительная длина КР
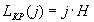 (18)
(18)
Подставляя (18) в (17) и затем в (16), получим, что
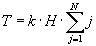
Сумма арифметической прогрессии
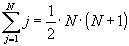
Таким образом, время кодирования всей перестановки
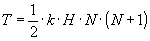 (19)
(19)
пропорционально квадрату ее длины N.
При декодировании характер
зависимости остается тот же. Изменяется лишь
коэффициент пропорциональности k. К настоящему времени разработаны
программы нумерационных кодера и декодера на
языке ассемблера для персонального компьютера
типа IBM PC, позволяющие менять
размер КР от 4 байт до 64 Кбайт. Для разработанных
программ коэффициент k
при кодировании равен 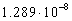 сек/бит, а при
декодировании
сек/бит, а при
декодировании 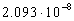 сек/бит (AMD-K6 200 МГц). Необходимо отметить, что для
программ, написанных на разных языках
программирования и для разных операционных
систем, будет меняться только коэффициент k, но не общая зависимость времени
кодирования T от длины
последовательности N.
сек/бит (AMD-K6 200 МГц). Необходимо отметить, что для
программ, написанных на разных языках
программирования и для разных операционных
систем, будет меняться только коэффициент k, но не общая зависимость времени
кодирования T от длины
последовательности N.
Очевидно, что одну и ту же
последовательность длиной N можно кодировать разными способами:
либо обрабатывать ее целиком, либо разбить на 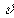 равных участков длиной N/
равных участков длиной N/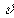 и каждый
из них обрабатывать отдельно. В последнем случае
представляет интерес оптимальное число
и каждый
из них обрабатывать отдельно. В последнем случае
представляет интерес оптимальное число 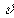 ,
, 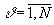 , таких
участков, при котором время, затраченное на
кодирование всей перестановки длиной N, будет минимальным.
, таких
участков, при котором время, затраченное на
кодирование всей перестановки длиной N, будет минимальным.
Попробуем определить оптимальное
значение 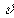 или покажем, что его не существует.
Действительно, время обработки всей
последовательности длиной N является суммой времен обработки
каждого из
или покажем, что его не существует.
Действительно, время обработки всей
последовательности длиной N является суммой времен обработки
каждого из 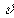 интервалов, т.е.
интервалов, т.е.
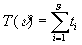 (20)
(20)
Время обработки каждого отдельного интервала согласно (19)
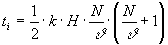 (21)
(21)
Подставляя (21) в (20), находим
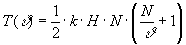 (22)
(22)
Как видно из полученного выражения
оптимального значения 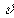 не существует.
Время кодирования перестановки максимально при
не существует.
Время кодирования перестановки максимально при 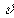 =1
и минимально при
=1
и минимально при 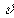 =N. В последнем
случае зависимость между временем кодирования и
длиной последовательности становится линейной,
однако исчезает эффект сжатия информации.
=N. В последнем
случае зависимость между временем кодирования и
длиной последовательности становится линейной,
однако исчезает эффект сжатия информации.
Заключение
Оптимальные свойства алгоритма начинают проявляться при достаточно длинной последовательности, а, следовательно, большой величине КР. Но при этом сильно возрастает время обработки. Например, при размере КР, равном 64 Кбайт, на компьютере с процессором INTEL PENTIUM 133 МГц время, затрачиваемое на кодирование, составляет 14 минут, а на декодирование 23 минуты (при длине последовательности 112 тыс. байт, текст на русском языке). Количество перестановок с повторениями в этом случае измеряется двоичным числом, занимающим 64 Кбайт. В связи с этим широкое распространение этого алгоритма в системах сжатия информации весьма проблематично.
Другой проблемой данного алгоритма является то, что для распаковки последовательности наряду с КР необходим также КС. При небольших размерах сжимаемого блока данных это приводит к неэффективности использования данного алгоритма по сравнению с адаптивными версиями Хаффмановского и арифметического кодеров.
Список литературы
Сведения об авторе
Лобанов Сергей Викторович, аспирант кафедры 402 радиосистем управления и передачи информации Московского государственного авиационного института (технического университета)
Телефон: 904-20-36
E-mail: sergey@degunino.net