УДК: 621.391.1
Повышение эффективности системы
фазовой автоподстройки навигационного
приемника при работе в условиях кратковременных
замираний сигнала
П.М. Язев
В работе исследуется поведение системы
фазовой автоподстройки (ФАП) третьего порядка
астатизма при наличии помех в виде нормального
шума и кратковременных замираний сигнала.
Приводится методика для оценки вероятностей
самостоятельного возобновления слежения и
перескока фазы по окончании замирания. Даются
рекомендации по повышению эффективности системы
ФАП навигационного приемника, работающего в
условиях кратковременных замираний.
Введение. Постановка задачи.
Синхронизация и демодуляция несущего
колебания в аппаратуре потребителя (в
навигационном приемнике) систем спутниковой
радионавигации осуществляется с помощью
цифровой системы ФАП [1], которая
зачастую реализуется в виде петли третьего
порядка астатизма. Использование ФАП третьего
порядка обусловлено требованиями малой
динамической ошибки при слежении за фазой
сигнала, частота которого изменяется из-за
доплеровского эффекта, а также требованиями
уменьшения эквивалентной шумовой полосы.
Система ФАП работает в тяжелой помеховой
обстановке, связанной с низким энергетическим
потенциалом. Установка навигационного приемника
на подвижном объекте приводит к ухудшению
условий работы ФАП из-за появления
кратковременных замираний сигнала, связанных с
попаданием приемника в область радиотени.
Рассмотрим особенности работы системы ФАП
третьего порядка астатизма, эквивалентная схема
которой представлена на рис. 1, в указанных
условиях. На рис. 1 приняты следующие обозначения:
 с(t)
- фаза входного сигнала;
с(t)
- фаза входного сигнала;  оп(t) - фаза опорного сигнала, вырабатываемого системой ФАП;
оп(t) - фаза опорного сигнала, вырабатываемого системой ФАП;  (t)=
(t)=  с(t)-
с(t)- оп(t) -
ошибка слежения;
оп(t) -
ошибка слежения; 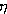 э(t) -
эквивалентный шум, который определяется шумовой компонентой
сигнала ошибки дискриминатора, усредненной за
период регулирования. Дискриминационная
характеристика полагается пилообразной с
апертурой
э(t) -
эквивалентный шум, который определяется шумовой компонентой
сигнала ошибки дискриминатора, усредненной за
период регулирования. Дискриминационная
характеристика полагается пилообразной с
апертурой 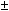
 /2. Такая характеристика соответствует
арктангенсному дискриминатору ФАП [1],
[2] .
/2. Такая характеристика соответствует
арктангенсному дискриминатору ФАП [1],
[2] .
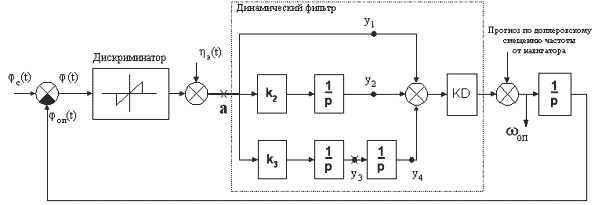
Рис.1. Эквивалентная схема исследуемой
ФАП
Если ФАП находится в режиме слежения, то
величины в каждой точке динамического фильтра
(рис. 1) имеют случайную и регулярную компоненты,
т.е. их можно представить в виде:
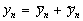 (1)
(1)
где n - индекс, n=1...4; 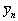 - регулярная компонента;
- регулярная компонента; 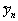 -
случайная компонента. Случайная компонента
обусловлена воздействием случайных процессов,
главным образом теплового шума. Регулярная
компонента зависит от параметров навигационного
сигнала.
-
случайная компонента. Случайная компонента
обусловлена воздействием случайных процессов,
главным образом теплового шума. Регулярная
компонента зависит от параметров навигационного
сигнала.
Будем считать, что на достаточно
большом интервале времени изменение фазы
сигнала из-за взаимного движения навигационного
спутника и приемника друг относительно друга
можно описать полиномом второй степени:
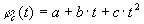 (2)
(2)
где a, b, c - константы.
Константа b - пропорциональна доплеровскому
смещению частоты, с - пропорциональна
скорости изменения частоты. Тогда, если на входе
ФАП имеется сигнал с постоянной частотой, что в
модели (2) соответствует равенству нулю параметра
с и не равенству нулю параметров a и b, то
после окончания переходных процессов в петле
регулярные компоненты в точках y2 и y3
будут нулевыми, а регулярная компонента в точке y4
будет равна b/KD, где KD - параметр
эквивалентной схемы ФАП.
Если на вход ФАП подать сигнал, частота
которого изменяется по линейному закону (параметр
с в (2) отличен от нуля), то при отсутствии прогноза
регулярная компонента в точке y3 будет
равна c/KD, в точке y4 будет изменяться
по закону сt/KD.
Нетрудно заметить, что наличие
регулярных компонент позволяет петле ФАП
компенсировать изменение фазы сигнала в момент
его отсутствия при замирании. Действительно,
если предположить, что случайные воздействия на
входе ФАП отсутствуют, а фаза сигнала изменяется
по закону (2), то в течение интервала замирания
ошибка слежения изменяться не будет
(предполагается, что переходной процесс в петле
завершился до начала замирания).
Однако, наличие случайных компонент на
интеграторах динамического фильтра в случае
замирания приводит к паразитному уходу частоты
опорного генератора. При этом, величина ухода
частоты является случайной. Ее дисперсия зависит
от продолжительности замирания и интенсивности
случайного воздействия.
При появлении сигнала начальная
расстройка (т.е. разница между частотой сигнала и
частотой опорного генератора) может оказаться
больше или меньше полосы захвата системы ФАП. В
первом случае самостоятельный переход системы в
синхронизм не возможен - происходит срыв
слежения. Во втором случае происходит втягивание
системы в синхронизм с дальнейшим слежением. При
этом возможно попадание в ту же точку
устойчивого равновесия (разность полных фаз
генератора и сигнала остается такой же, как в
момент до пропадания сигнала) , а так же перескок
фазы (разность фаз изменяется на 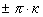 (k=1,2..).
Наступление того или иного исхода случайно и может быть
охарактеризовано вероятностью.
(k=1,2..).
Наступление того или иного исхода случайно и может быть
охарактеризовано вероятностью.
Срыв слежения и перескок фазы являются
нежелательными событиями в работе
навигационного приемника. Первое событие
приводит к дополнительным затратам времени на
поиск сигнала, которые могут составить несколько
десятков секунд. Второе событие может приводить
к ошибкам местоопределения или к дополнительным
затратам времени для разрешения неоднозначности
при осуществлении фазовых измерений.
Таким образом, работа петли ФАП при
наличии замираний должна по возможности
сопровождаться как можно меньшими затратами
времени на процедуру возобновления слежения по
окончании замирания. Данная проблема наиболее
просто решается в случае неподвижного
навигационного приемника. При этом достаточно
произвести размыкание в цепи памяти по ускорению
динамического фильтра (в точке y3) на
время замирания. Такое размыкание избавит от
паразитного изменения частоты опорного
генератора ФАП. В этом режиме необходимо также
осуществлять ввод в петлю прогноза по
доплеровскому смещению, связанному с движением
навигационного спутника (см. рис. 1).
В случае, если ускорение
навигационного приемника таково, что уход
частоты сигнала за время замирания может
превысить полосу захвата ФАП размыкание цепи
памяти по ускорению является нецелесообразным. В
этом случае повысить эффективность ФАП можно,
оценив продолжительности замираний, при которых
еще c высокой вероятностью возможно
самостоятельное возобновление слежения и
возобновление слежения без перескока фазы.
Получение указанных оценок является целью
данной работы.
В соответствии с этим задача может
быть сформулирована следующим образом. На входе
цифровой системы ФАП третьего порядка астатизма
имеется смесь сигнала и нормального шума.
Энергетический потенциал задан. Фаза сигнала
изменяется в соответствии с (2). Система ФАП
находится в режиме слежения, т.е. переходные
процессы завершились. Происходит замирание
сигнала, момент которого в приемнике фиксируется
специальным индикатором. Для предотвращения
управления частотой опорного генератора шумами
при отсутствии сигнала петлю ФАП на время
замирания разрывают в точке "a" (см. рис. 1).
Требуется оценить вероятность самостоятельного
возобновления слежения и вероятность перескока
фазы в случае возобновления слежения при
известной продолжительности замирания.
Теоретический анализ.
Как уже было указано, паразитное
изменение частоты опорного генератора ФАП
связано с наличием случайных составляющих на
интеграторах динамического фильтра. Поэтому при
анализе ФАП с целью определения вероятностей
самозахвата и перескока фазы будем полагать, что 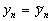 .
.
Обозначив индексом 1 величины в момент
пропадания, а индексом 2 - в момент появления
сигнала, можно записать начальное условие для
ФАП в момент окончания замирания
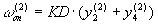 (3)
(3)
где  оп - относительная (относительно
частоты сигнала) частота опорного генератора в
рассматриваемой модели ФАП; KD - параметр ФАП.
Поскольку y2 и y3 не изменяются
за время перерыва, соотношение (3) можно записать
в виде
оп - относительная (относительно
частоты сигнала) частота опорного генератора в
рассматриваемой модели ФАП; KD - параметр ФАП.
Поскольку y2 и y3 не изменяются
за время перерыва, соотношение (3) можно записать
в виде
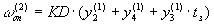 (4)
(4)
где tз- продолжительность
замирания.
В соотношение (4) входят случайные
величины, поэтому  оп также будет являться
случайной величиной. Поскольку было задано, что
шум на входе ФАП является нормальным, а величина
самой частоты определяется как линейная
комбинация величин на выходе интеграторов
динамического фильтра, то закон распределения
частоты
оп также будет являться
случайной величиной. Поскольку было задано, что
шум на входе ФАП является нормальным, а величина
самой частоты определяется как линейная
комбинация величин на выходе интеграторов
динамического фильтра, то закон распределения
частоты  оп
будет также являться нормальным. Дисперсию
оп
будет также являться нормальным. Дисперсию  оп
на момент появления сигнала можно определить с
помощью соотношения
оп
на момент появления сигнала можно определить с
помощью соотношения
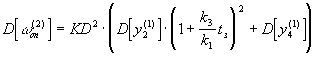 (5)
(5)
где D[.] - оператор
определения дисперсии. При выводе (5) учитывалось,
что D[y3]=D[y2](k3/k1)2
и y4 независимо от y2 в один
момент времени.
Величина ошибки слежения по фазе на
момент окончания замирания также является
случайной величиной и имеет нормальный закон
распределения. Если предположить, что ошибка
слежения по фазе в момент наступления замирания
была мала, можно записать соотношение для
расчета дисперсии рассогласования по фазе на
момент появления сигнала
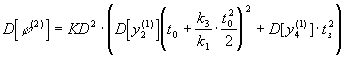 (6)
(6)
Спектральная плотность эквивалентных
флуктуаций 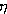 э(t), связанных с наличием
теплового шума на входе системы ФАП определяется
соотношением
э(t), связанных с наличием
теплового шума на входе системы ФАП определяется
соотношением
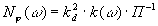 (7)
(7)
где kd - крутизна
дискриминационной характеристики вблизи
рабочей точки (безразмерная), для исследуемой ФАП
kd=1; П - энергетический потенциал на
входе ФАП; k( ) - коэффициент, определяющий
спектральную плотность усредненного шума при
цифровой реализации ФАП
) - коэффициент, определяющий
спектральную плотность усредненного шума при
цифровой реализации ФАП
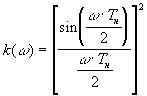 (8)
(8)
где Tн - время усреднения
(величина, обратная частоте регулирования в
петле ФАП).
Дисперсия случайной составляющей в
произвольной точке эквивалентной схемы ФАП (рис. 1)
может быть рассчитана с помощью соотношения
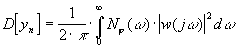 (9)
(9)
где w(j ) - комплексная передаточная
функция с точки приложения случайного
воздействия
) - комплексная передаточная
функция с точки приложения случайного
воздействия 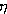 э(t) на выход yn.
Для расчета дисперсий в точках y2, y4
по (9) при действии на систему ФАП шума
э(t) на выход yn.
Для расчета дисперсий в точках y2, y4
по (9) при действии на систему ФАП шума 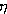 э(t)
передаточные функции определяются
соотношениями
э(t)
передаточные функции определяются
соотношениями
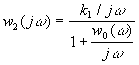
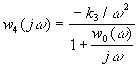
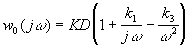 (10)
(10)
Параметры ФАП k1, k3 и
KD выбираются в соответствии с рекомендациями
[2]
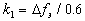 ,
, 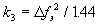 ,
,
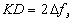 (11)
(11)
где  fэ √ эквивалентная шумовая
полоса ФАП.
fэ √ эквивалентная шумовая
полоса ФАП.
Поскольку на систему ФАП действует
случайный процесс, то вероятность наступления
синхронизма по окончании замирания будет
зависеть не только от начальной расстройки, но
также и от многих других факторов, среди которых
величина энергетического потенциала, форма
дискриминационной характеристики, порядок
астатизма, определения самого события захвата
(например, захват может считаться произошедшим,
если ошибка слежения достигла некоторой
величины за некоторое время). В целом для ФАП
можно ввести характеристику Pзахв.ФАП( оп),
которая определяет вероятность наступления
синхронизма в системе ФАП при некоторой
начальной отстройке
оп),
которая определяет вероятность наступления
синхронизма в системе ФАП при некоторой
начальной отстройке  оп. Тогда можно записать
оп. Тогда можно записать
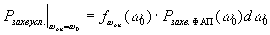 (12)
(12)
где Pзахв.усл. - вероятность
самозахвата в системе ФАП при условии  оп=
оп=  0;
0;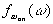 - закон
распределения относительной частоты опорного
генератора
- закон
распределения относительной частоты опорного
генератора  оп
на момент окончания замирания;
оп
на момент окончания замирания; 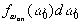 -
вероятность того, что опорный генератор будет
иметь на момент окончания замирания частоту
-
вероятность того, что опорный генератор будет
иметь на момент окончания замирания частоту  0.
Безусловную вероятность самозахвата ФАП
определяем путем интегрирования правой части (12)
и умножения результата на два (поскольку интерес
представляет модуль отстройки)
0.
Безусловную вероятность самозахвата ФАП
определяем путем интегрирования правой части (12)
и умножения результата на два (поскольку интерес
представляет модуль отстройки)
 (13)
(13)
где  мах - максимальная отстройка при
которой еще возможен захват в системе ФАП.
мах - максимальная отстройка при
которой еще возможен захват в системе ФАП.
Производя аналогичные рассуждения
относительно перескока фазы получаем
соотношение для расчета вероятности его
появления
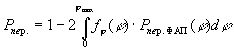 (14)
(14)
где 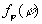 -
закон распределения ошибки слежения на момент
окончания замирания; Pпер.ФАП(
-
закон распределения ошибки слежения на момент
окончания замирания; Pпер.ФАП( ) - вероятность
перескока фазы при начальной ошибке
) - вероятность
перескока фазы при начальной ошибке  ;
;  maxмаксимальная
ошибка слежения, при которой
maxмаксимальная
ошибка слежения, при которой 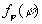 отлична от нуля.
отлична от нуля.
Для аналоговой ФАП первого порядка
характеристики Pзахв.ФАП( оп) и Pпер.ФАП(
оп) и Pпер.ФАП( ) могут быть точно определены путем решения
уравнения Фокера-Планка [3] . Для
аналоговой ФАП второго и третьего порядков
астатизма указанная задача пока не имеет точного
решения [3] , [4] . Данная
задача также не решена для дискретных систем
любого порядка. Для получения характеристик
захвата и перескока в дискретных системах можно
воспользоваться методиками, которые
предполагают анализ дискретных систем в
непрерывном приближении [4] , или
имитационным моделированием.
) могут быть точно определены путем решения
уравнения Фокера-Планка [3] . Для
аналоговой ФАП второго и третьего порядков
астатизма указанная задача пока не имеет точного
решения [3] , [4] . Данная
задача также не решена для дискретных систем
любого порядка. Для получения характеристик
захвата и перескока в дискретных системах можно
воспользоваться методиками, которые
предполагают анализ дискретных систем в
непрерывном приближении [4] , или
имитационным моделированием.
Таким образом, определение
характеристик Pзахв.ФАП( оп) и Pпер.ФАП(
оп) и Pпер.ФАП( ) может рассматриваться как самостоятельная
задача, которая требует дополнительных
исследований. Однако, возможен и приближенный
подход.
) может рассматриваться как самостоятельная
задача, которая требует дополнительных
исследований. Однако, возможен и приближенный
подход.
Известно, что для ФАП третьего порядка
астатизма полоса захвата ограничена лишь
пределами перестройки частоты генератора.
Однако, при увеличении начальной расcтройки на
величину, большую шумовой полосы системы, резко
увеличивается время необходимое для вхождения в
синхронизм [2] , [3].
Поэтому, для ФАП третьего порядка можно положить,
что
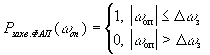 (15)
(15)
где 
 з=2
з=2
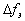 имеет
смысл полосы захвата. Если флуктуационная
ошибка ФАП не очень велика можно также считать,
что:
имеет
смысл полосы захвата. Если флуктуационная
ошибка ФАП не очень велика можно также считать,
что:
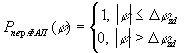 (16)
(16)
где 
 zd
равна половине апертуры (области притяжения к
одной устойчивой точке) дискриминационной
характеристики. Для исследуемой системы
zd
равна половине апертуры (области притяжения к
одной устойчивой точке) дискриминационной
характеристики. Для исследуемой системы 
 zd=
zd= /2.
/2.
При выборе характеристик захвата и
перескока (15), (16) вероятности самозахвата и
перескока фазы после окончании замирания
рассчитываются следующим образом:
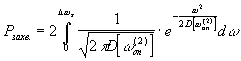 (17)
(17)
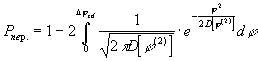 (18)
(18)
Далее в работе будет произведено
исследование ФАП как с использованием
приближенной расчетной методики, когда при
определении вероятностей самозахвата и
перескока фазы выбор характеристик Pзахв.ФАП( 0) и
Pпер.ФАП(
0) и
Pпер.ФАП( 0) производится в
соответствии с (15) и (16), так и с использованием
расчетно-модельной методики, когда
характеристики Pзахв.ФАП(
0) производится в
соответствии с (15) и (16), так и с использованием
расчетно-модельной методики, когда
характеристики Pзахв.ФАП( 0) и Pпер.ФАП(
0) и Pпер.ФАП( 0)
определяются на имитационной модели ФАП.
0)
определяются на имитационной модели ФАП.
Анализ ФАП с использованием
приближенной расчетной методики.
Некоторые результаты расчета
вероятности самозахвата (17) приведены на рис. 2.
Расчет был произведен для дискретной системы ФАП
с частотой регулирования 200 Гц, что соответствует
времени усреднения Tн=0.005 сек. Расчет
производился для двух типовых значений
энергетических потенциалов П=30 дБГц, П=40 дБГц и
двух значений шумовых полос  fэ=10 Гц и
fэ=10 Гц и  fэ
=2Гц (рассчитанные зависимости рис. 2 помечены
соответствующими значениями энергетических
потенциалов и шумовых полос).
fэ
=2Гц (рассчитанные зависимости рис. 2 помечены
соответствующими значениями энергетических
потенциалов и шумовых полос).
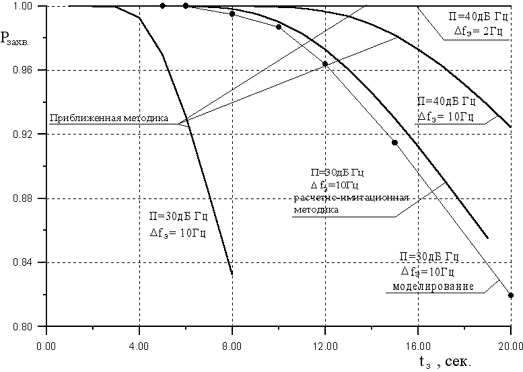
Рис. 2. Результаты оценки вероятности
самозахвата
Результаты расчета позволяют сделать
выводы о допустимой длительности замирания, по
окончании которого с большой вероятностью
система ФАП самостоятельно возобновит слежение.
Так, например, если П=40 дБГц и  fэ
=10 Гц, то можно говорить о вероятности
самозахвата не меньше 0.96, если время замирания не
превысит 17 сек. Если произвести сужение шумовой
полосы до
fэ
=10 Гц, то можно говорить о вероятности
самозахвата не меньше 0.96, если время замирания не
превысит 17 сек. Если произвести сужение шумовой
полосы до  fэ=2 Гц, то как показал
расчет, при временах замирания 20...30 сек. срывов
слежения наблюдаться практически не будет.
fэ=2 Гц, то как показал
расчет, при временах замирания 20...30 сек. срывов
слежения наблюдаться практически не будет.
На рис. 3 приведены некоторые
результаты расчета вероятности перескока фазы
(18) для исследуемой системы ФАП. На основании
указанных зависимостей можно оценить
продолжительность замирания, при котором
вероятность перескока мала. Например, если П=40
дБГц и  fэ =2 Гц перескоки
практически не будут наблюдаться при времени
замирания до 4 сек.
fэ =2 Гц перескоки
практически не будут наблюдаться при времени
замирания до 4 сек.
Таким образом, поиск сигнала в
навигационном приемнике целесообразно начинать
не сразу после его пропадания, а с некоторой
задержкой. Величина задержки определяется
продолжительностью замирания, по окончании
которого с достаточно высокой вероятностью еще
возможно самостоятельное возобновление
слежения. Если сигнал появился, и слежение
возобновилось до истечения интервала задержки,
решение о необходимости процедуры разрешения
неоднозначности может быть принято на основании
информации о продолжительности замирания и
статистики перескока как функции времени
замирания. Если сигнал не появился в течении
интервала задержки, необходимо приступать к
процедурам поиска. Использование описанного
алгоритма работы ФАП позволит уменьшить
суммарные затраты времени на процедуры поиска
сигнала и разрешения неоднозначностей фазовых
измерений при преобладании кратковременных
замираний сигнала.
На рис. 2 и 3 приведены также результаты
моделирования. Их обсуждение будет произведено
далее.
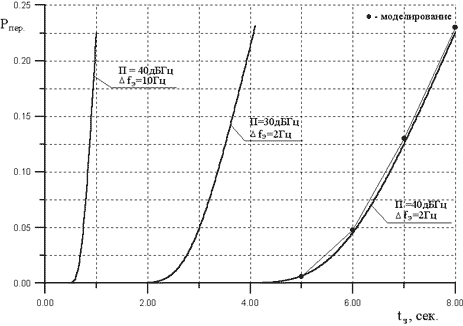
Рис. 3. Результаты оценки вероятности
перескока фазы
Анализ ФАП с использованием
расчетно-имитационной методики.
Оценка достоверности предлагаемых
методик.
Для определения статистических
характеристик ФАП по захвату и перескоку Pзахв.ФАП( оп) и
Pпер.ФАП(
оп) и
Pпер.ФАП( ) на основе эквивалентной схемы
рис. 1 была разработана имитационная модель. При
построении имитационной модели возникает задача
выбора алгоритма работы индикатора захвата. Для
решения этой задачи было произведено
исследование явления захвата при наличии шума.
Указанные исследования производились для
дискретной системы ФАП (
) на основе эквивалентной схемы
рис. 1 была разработана имитационная модель. При
построении имитационной модели возникает задача
выбора алгоритма работы индикатора захвата. Для
решения этой задачи было произведено
исследование явления захвата при наличии шума.
Указанные исследования производились для
дискретной системы ФАП ( fэ =10 Гц,
частота регулирования 200 Гц) третьего порядка
астатизма, на вход которой подавалась смесь
сигнала и шума. При этом фиксировалась частота
сигнала и энергетический потенциал. Было
отмечено следующее:
fэ =10 Гц,
частота регулирования 200 Гц) третьего порядка
астатизма, на вход которой подавалась смесь
сигнала и шума. При этом фиксировалась частота
сигнала и энергетический потенциал. Было
отмечено следующее:
- наступление захвата имело случайный
характер и зависело от двух факторов - отстройка
сигнала по частоте и энергетический потенциал;
- захват либо происходил в течении 1...2
сек., либо не происходил вообще. В последнем
случае на выходе дискриминатора наблюдались
непрекращающиеся биения. Зависимости времени
установления от величины начальной расстройки,
характерной для аналоговой ФАП [3] ,отмечено
не было. Данный факт можно объяснить тем, что при
таком соотношении шумовой полосы и частоты
регулирования дискретная ФАП не обладает
свойствами, характерными для аналоговой ФАП.
По результатам проведенного
исследования был выбран следующий алгоритм
работы индикатора захвата (критерий захвата).
После окончания замирания (в имитационной
модели) выдерживалась пауза равная tуст
=2 сек. По окончании паузы производилось
измерение ошибки слежения  (tуст). Далее,
если в течении интервала времени 2.tуст
модуль ошибки слежения
(tуст). Далее,
если в течении интервала времени 2.tуст
модуль ошибки слежения  (t) превышал величину
(t) превышал величину  /2, то
делался вывод о том, что возобновления слежения
не произошло. В противном случае считалось, что
слежение возобновилось. В этом случае
вычислялась разность ошибок слежения до
замирания и по окончании процесса установления.
Если модуль разности превышал величину
/2, то
делался вывод о том, что возобновления слежения
не произошло. В противном случае считалось, что
слежение возобновилось. В этом случае
вычислялась разность ошибок слежения до
замирания и по окончании процесса установления.
Если модуль разности превышал величину  /2, то
делался вывод о перескоке фазы.
/2, то
делался вывод о перескоке фазы.
Далее на модели были определены
характеристики Pзахв.ФАП( ) и Pпер.ФАП(
) и Pпер.ФАП( ), которые
представлены на рис. 4 и рис. 5. Из анализа рис. 5
следует, что ФАП может обеспечивать захват,
критерий которого определен выше, при начальных
расстройках больших, чем шумовая полоса системы.
Причем, уменьшение энергетического потенциала
способствует увеличению вероятности захвата
(данный факт в некоторой степени согласуется с
результатами исследований ФАП первого порядка
астатизма [3] , согласно которым
уменьшение отношения сигнал-шум приводит к
уменьшению длительности переходного процесса). В
целом по зависимостям рис. 4 невозможно четко
определить полосу захвата, т.е. нельзя определить
диапазоны начальных расстроек, при которых
всегда (с большой вероятностью) будет или не
будет наблюдаться захват. В тоже время по
зависимостям рис. 5 можно определить пороговую
величину начальной ошибки слежения, превышение
которой приведет к перескоку. Данный факт
подтверждает допустимость определения
характеристики Pпер.ФАП(
), которые
представлены на рис. 4 и рис. 5. Из анализа рис. 5
следует, что ФАП может обеспечивать захват,
критерий которого определен выше, при начальных
расстройках больших, чем шумовая полоса системы.
Причем, уменьшение энергетического потенциала
способствует увеличению вероятности захвата
(данный факт в некоторой степени согласуется с
результатами исследований ФАП первого порядка
астатизма [3] , согласно которым
уменьшение отношения сигнал-шум приводит к
уменьшению длительности переходного процесса). В
целом по зависимостям рис. 4 невозможно четко
определить полосу захвата, т.е. нельзя определить
диапазоны начальных расстроек, при которых
всегда (с большой вероятностью) будет или не
будет наблюдаться захват. В тоже время по
зависимостям рис. 5 можно определить пороговую
величину начальной ошибки слежения, превышение
которой приведет к перескоку. Данный факт
подтверждает допустимость определения
характеристики Pпер.ФАП( ) в соответствии с (16).
) в соответствии с (16).
С помощью полученной характеристики Pзахв.ФАП( ) был
произведен расчет вероятности самозахвата (13)
для ФАП с
) был
произведен расчет вероятности самозахвата (13)
для ФАП с  fэ=10 Гц при П=30 дБГц. Результаты
расчета представлены на рис. 2 (кривая с надписью
"расчетно-имитационная методика").
fэ=10 Гц при П=30 дБГц. Результаты
расчета представлены на рис. 2 (кривая с надписью
"расчетно-имитационная методика").
С помощью имитационной модели была
произведена непосредственная оценка
вероятностей самозахвата и перескока фазы.
Некоторые результаты оценки приведены на рис. 2 и
3 (зависимости отмеченные кружочками).
Из сопоставления результатов
моделирования и расчета по двум предлагаемым
методикам можно сделать следующие выводы:
- расчетно-имитационная методика
обеспечивает высокую достоверность при
оценивании вероятности самозахвата. Некоторое
несовпадение результатов расчета с результатами
моделирования при использовании данной методики
объясняется следующим образом. Параметры
имитационной модели выбирались в соответствии с
соотношениями (11), которые справедливы для
квазинепрерывной модели ФАП. Дискретная модель
ФАП с параметрами, выбранными аналогичным
образом, будет иметь несколько большую
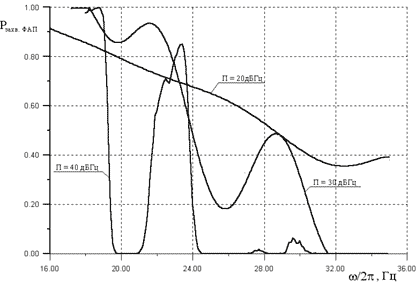
Рис. 4. Вероятность вхождения в
синхронизм системы ФАП
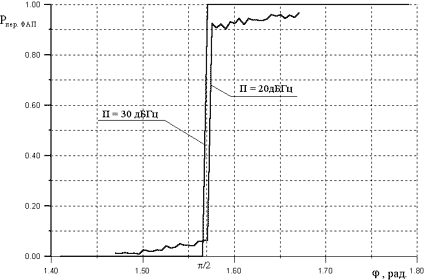
Рис. 5. Вероятность перескока фазы в
системе ФАП
эквивалентную шумовую полосу и
соответственно большую дисперсию величины  оп
на момент окончания замирания. Это приводит к
тому, что при фиксированном времени замирания
расчетная вероятность самозахвата оказывается
несколько больше аналогичной величины,
полученной на имитационной модели.
оп
на момент окончания замирания. Это приводит к
тому, что при фиксированном времени замирания
расчетная вероятность самозахвата оказывается
несколько больше аналогичной величины,
полученной на имитационной модели.
- приближенная методика обеспечивает
высокую точность только при оценивании
вероятности перескока фазы. При оценке
вероятности самозахвата результаты
эксперимента существенно не соответствуют
результатам расчета. Сопоставление результатов
моделирования и расчета показало, что у системы ФАП,
которую представляли в виде имитационной модели,
высокая вероятность самозахвата сохраняется при
времени замирания примерно в 2...2.5 раза большем,
чем дает расчет. Поэтому, можно говорить о том,
что захват в реальной ФАП будет обеспечиваться
при времени замирания гарантированно большем,
чем дает расчет с использованием приближенной
методики.
Выводы.
Работа системы ФАП навигационного
приемника в условиях кратковременных замираний
может характеризоваться двумя показателями
качества: вероятностью самостоятельного
вхождения в синхронизм и вероятностью перескока
фазы. Для определения указанных показателей
предлагается две методики: приближенная
расчетная и расчетно-имитационная.
При использовании приближенной
методики статистические показатели по захвату и
перескоку определяются через такие параметры
ФАП, как полоса захвата и апертура
дискриминационной характеристики. Полоса
захвата при этом полагается равной
эквивалентной шумовой полосе. Приближенная
методика обеспечивает инженерную точность
только при оценке вероятности перескока фазы.
Проведенные исследования показали, что высокая
вероятность самозахвата на практике будет
обеспечиваться при гарантированно большем
времени замирания, чем дает расчет с
использованием приближенной методики.
Для получения более достоверной
оценки вероятности самозахвата необходимо
использовать расчетно-модельную методику,
которая основывается на информации о
вероятности вхождения в синхронизм петли ФАП в
зависимости от начальных условий при наличии
случайного возмущения. Для дискретной ФАП
третьего порядка астатизма такая информация
может быть получена с помощью имитационного
моделирования.
Повышение эффективности системы ФАП
может быть произведено путем уменьшения затрат
времени на дополнительный поиск сигнала и
разрешение неоднозначности фазовых измерений по
окончании замирания. Для этого необходимо
произвести оценку продолжительности замирания,
при котором с достаточно высокой вероятностью
возможно самостоятельное возобновление
слежения и возобновление слежения без перескока
фазы.
Список литературы.
- Глобальная спутниковая радионавигационная
система ГЛОНАСС // под ред. В.Н. Харисова, А.И.
Перова, В.А. Болдина. -М.: ИПРЖР, 1998. - 400 с.
- Жодзишский М.И. Цифровые радиоприемные
системы: Справочник. - М.:Радио и связь, 1990 . - 207 с.
- Линдсей В. Системы синхронизации в связи и
управлении. - М.:Советское радио, 1978. - 598 с.
- Шахгильдян В.В., Ляховкин А.А.,Карякин В.Л.
Системы фазовой синхронизации с элементами
дискритизации. - М.: Радио и связь, 1989. - 320 с.
Сведения об авторе.
Язев Павел Михайлович, аспирант кафедры радиосистем передачи информации и управления Московского
государственного авиационного института (технического университета).
 с(t)
- фаза входного сигнала;
с(t)
- фаза входного сигнала;  оп(t) - фаза опорного сигнала, вырабатываемого системой ФАП;
оп(t) - фаза опорного сигнала, вырабатываемого системой ФАП;  (t)=
(t)=  с(t)-
с(t)- оп(t) -
ошибка слежения;
оп(t) -
ошибка слежения; 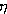 э(t) -
эквивалентный шум, который определяется шумовой компонентой
сигнала ошибки дискриминатора, усредненной за
период регулирования. Дискриминационная
характеристика полагается пилообразной с
апертурой
э(t) -
эквивалентный шум, который определяется шумовой компонентой
сигнала ошибки дискриминатора, усредненной за
период регулирования. Дискриминационная
характеристика полагается пилообразной с
апертурой 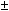
 /2. Такая характеристика соответствует
арктангенсному дискриминатору ФАП [1],
[2] .
/2. Такая характеристика соответствует
арктангенсному дискриминатору ФАП [1],
[2] .
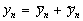 (1)
(1)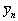 - регулярная компонента;
- регулярная компонента; 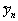 -
случайная компонента. Случайная компонента
обусловлена воздействием случайных процессов,
главным образом теплового шума. Регулярная
компонента зависит от параметров навигационного
сигнала.
-
случайная компонента. Случайная компонента
обусловлена воздействием случайных процессов,
главным образом теплового шума. Регулярная
компонента зависит от параметров навигационного
сигнала. 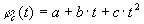 (2)
(2) 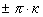 (k=1,2..).
Наступление того или иного исхода случайно и может быть
охарактеризовано вероятностью.
(k=1,2..).
Наступление того или иного исхода случайно и может быть
охарактеризовано вероятностью. 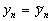 .
.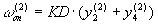 (3)
(3)  оп - относительная (относительно
частоты сигнала) частота опорного генератора в
рассматриваемой модели ФАП; KD - параметр ФАП.
Поскольку y2 и y3 не изменяются
за время перерыва, соотношение (
оп - относительная (относительно
частоты сигнала) частота опорного генератора в
рассматриваемой модели ФАП; KD - параметр ФАП.
Поскольку y2 и y3 не изменяются
за время перерыва, соотношение (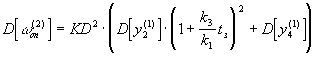 (5)
(5)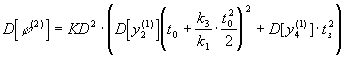 (6)
(6)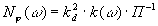 (7)
(7)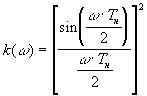 (8)
(8)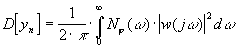 (9)
(9) 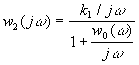
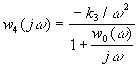
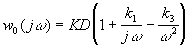 (10)
(10)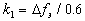 ,
, 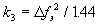 ,
,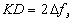 (11)
(11)  fэ √ эквивалентная шумовая
полоса ФАП.
fэ √ эквивалентная шумовая
полоса ФАП.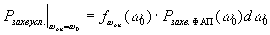 (12)
(12)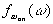 - закон
распределения относительной частоты опорного
генератора
- закон
распределения относительной частоты опорного
генератора 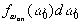 -
вероятность того, что опорный генератор будет
иметь на момент окончания замирания частоту
-
вероятность того, что опорный генератор будет
иметь на момент окончания замирания частоту  (13)
(13)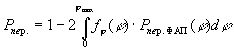 (14)
(14)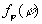 -
закон распределения ошибки слежения на момент
окончания замирания; Pпер.ФАП(
-
закон распределения ошибки слежения на момент
окончания замирания; Pпер.ФАП(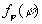 отлична от нуля.
отлична от нуля.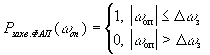 (15)
(15)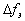 имеет
смысл полосы захвата. Если флуктуационная
ошибка ФАП не очень велика можно также считать,
что:
имеет
смысл полосы захвата. Если флуктуационная
ошибка ФАП не очень велика можно также считать,
что: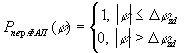 (16)
(16)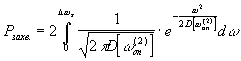 (17)
(17)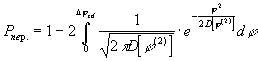 (18)
(18)


