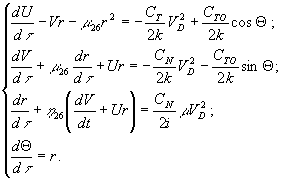 (1)
(1)УДК 629.734.7.015
Анализ колебаний парашютных систем, вызванных пульсацией купола
В.М. Чуркин, Д.А. Попов, Е.В. Серпичева
Исследуется реакция геометрически неизменяемой модели парашютной системы на пульсацию ее купола. Пульсация купола учитывается составляющей аэродинамической силы парашюта, которая с течением времени изменяется по гармоническому закону. Методом гармонической линеаризации определяются основные параметры и условия существования колебаний парашютной системы в диапазонах частот основного резонанса и частот субгармоник порядка 1/2 и 1/3.
Движение парашютных систем (ПС) на этапе спуска нередко сопровождается пульсацией купола - колебаниями купола, вызывающими периодическое изменение его формы и аэродинамических характеристик. Пульсация наблюдается при завершении процессов перецепки груза, раскрытия или разрифовки купола. Она может возникнуть под действием порывов ветра, аэродинамического следа от груза или в результате срыва вихрей с кромки купола. Явление пульсации неоднократно фиксировалось при проведении летных и стендовых испытаний ПС различной конструкции [1-3]. Рахматулин Х.А. и Рысев О.В., Королев В.М. и Рахматулин Х.А., Ильченко А.В. и Темненко В.А. в работах [4-6] аналитически исследовали условия возникновения пульсаций купола, рассматривая последние как колебания элемента ленты радиального каркаса, который находится под действием постоянного перепада давления.
Воздействие пульсации купола на динамику ПС с безинерционным парашютом изучалось в работах Фатыхова Ф.Ф. и Носарева И.М. [1,7]. В данной работе исследуется реакция ПС на пульсацию купола с использованием более сложной модели ПС, - геометрически неизменяемой ПС.
Движение геометрически неизменяемой ПС в вертикальной плоскости в осях связанной системы координат XOY можно описать следующей системой безразмерных уравнений, [8]
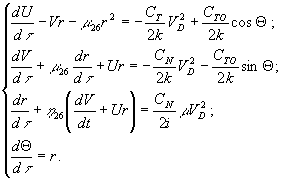 (1)
(1)
Здесь U, V √
проекции безразмерного вектора скорости центра
масс ПС на оси OX, OY; VD √
безразмерная скорость центра давления ПС; r √ безразмерная угловая скорость ПС;
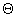 -
угол тангажа ПС; CT, CN √ коэффициенты касательной и
нормальной составляющих аэродинамической силы
купола; CТО √ значение
коэффициента CT при
установившемся снижении ПС;
-
угол тангажа ПС; CT, CN √ коэффициенты касательной и
нормальной составляющих аэродинамической силы
купола; CТО √ значение
коэффициента CT при
установившемся снижении ПС; 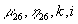 - безразмерные
параметры ПС, зависящие от коэффициентов
присоединенных масс купола;
- безразмерные
параметры ПС, зависящие от коэффициентов
присоединенных масс купола; 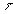 - безразмерное время.
- безразмерное время.
Следуя за авторами работ [1, 7]
предположим, что воздействие пульсации купола на
ПС проявляется в изменении аэродинамического
коэффициента СТ по гармоническому закону с
амплитудой а и частотой 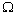 относительно
значения СТ = СТО
относительно
значения СТ = СТО
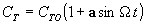 (2)
(2)
Подставим зависимость (2) в уравнения (1)
и запишем уравнения возмущенного движения ПС,
принимая в качестве невозмущенного движения
устойчивый спуск со скольжением. Полученную
систему заменим следующей системой упрощенных
уравнений возмущенного движения, в которой
учитывается нелинейная зависимость
коэффициента CN от угла
атаки 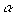
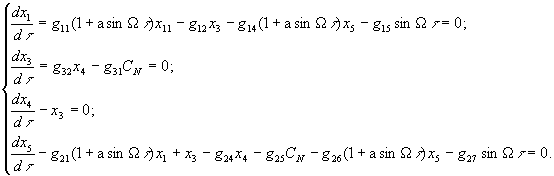 (3)
(3)
Здесь 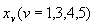 - возмущения переменных и
- возмущения переменных и 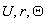
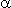 соответственно;
соответственно; 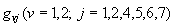 - постоянные
коэффициенты, зависящие от амплитуды а,
коэффициента СТО и параметров
- постоянные
коэффициенты, зависящие от амплитуды а,
коэффициента СТО и параметров 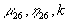 и
и 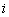 .
.
Уравнения системы (3) описывают
параметрически возбуждаемые нелинейные
колебания ПС, т.к. помимо нелинейной зависимости 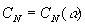 содержат
члены с периодически изменяющимися
коэффициентами. Предположим, что
содержат
члены с периодически изменяющимися
коэффициентами. Предположим, что
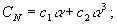
и будем искать решение системы (3) в виде
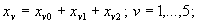 (4)
(4)
где
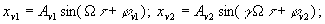
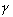 - порядок субгармонических
колебаний.
- порядок субгармонических
колебаний.
После гармонической линеаризации зависимости 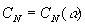 при
при 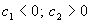 и членов с
периодически изменяющимися коэффициентами
будем иметь
и членов с
периодически изменяющимися коэффициентами
будем иметь
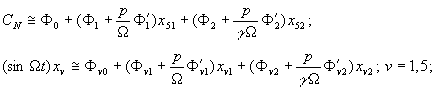
где
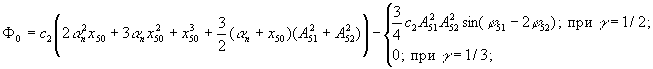
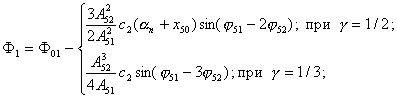
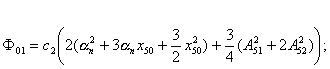
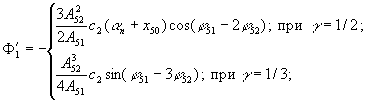
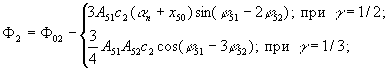
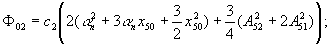
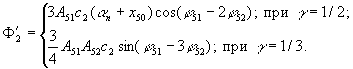
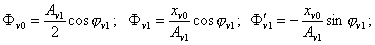
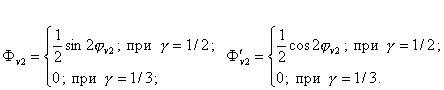
Получаемая линеаризованная система распадается на следующие системы, соответствующие постоянным и переменным составляющим искомого решения (4)
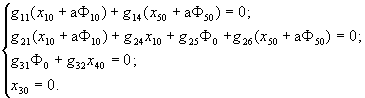 (5)
(5)
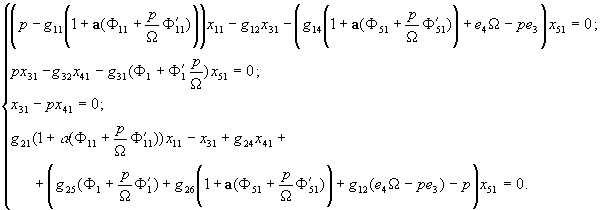 (6)
(6)
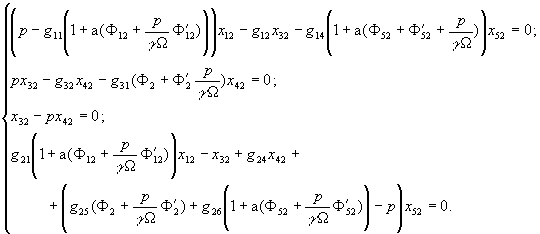 (7)
(7)
где 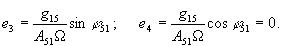
Отсюда записываем следующую систему трансцендентных уравнений
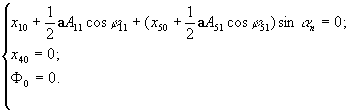 (8)
(8)
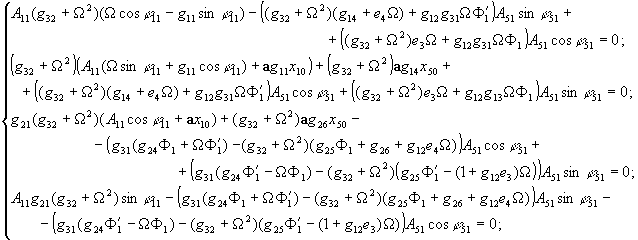 (9)
(9)
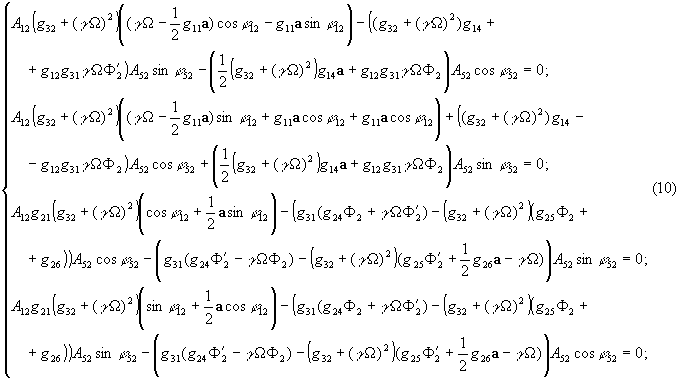
Характеристическое уравнение системы (6) можно представить в форме
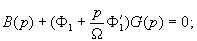 (11)
(11)
где
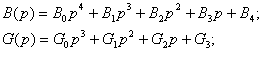
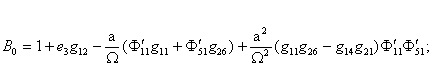
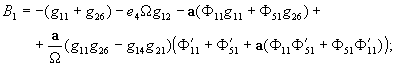
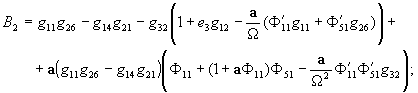
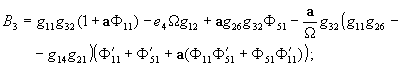
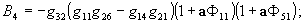
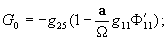
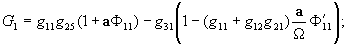
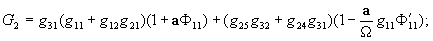
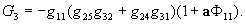
Полагая в уравнении (11) 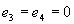 и заменив
и заменив 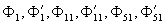 и
и  на
на 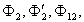
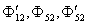 и
и 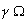 соответственно, получим
характеристическое уравнение системы (7).
соответственно, получим
характеристическое уравнение системы (7).
Уравнения (8) - (10) совместно с характеристическими уравнениями систем (6), (7) позволяют рассчитывать реакцию ПС на пульсацию купола, как в диапазоне частот основного резонанса, так и при резонансных частотах субгармонических колебаний порядка 1/2 и 1/3. Анализ устойчивости получаемых гармонических и субгармонических колебаний можно проводить, проверяя знаки коэффициентов соответствующих характеристических уравнений и выполнение следующего неравенства [9]
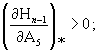
где Нn-1 √ предпоследний определитель Гурвица.
На рис. 1 изображены зависимости А51 = А51(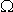 ), построенные по результатам
решения приведенных выше уравнений при
следующих значениях параметров ПС:
), построенные по результатам
решения приведенных выше уравнений при
следующих значениях параметров ПС: 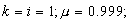
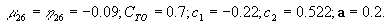 Зависимости рассчитаны
для нелинейной
Зависимости рассчитаны
для нелинейной
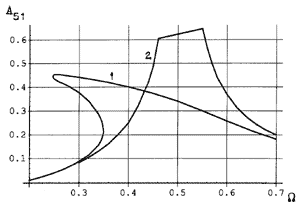
Рис.1. Амплитудно-частотные характеристики
нелинейной (кривая 1) и линейной (кривая 2) моделей ПС.
и линейной моделей ПС. У нелинейной
модели коэффициент CN
определяется выражением (5) и зависимость А51 = А51(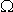 ) (кривая 1 на рис. 1) только
количественно отличается от соответствующей зависимости,
описывающей вынужденные колебания ПС [10] . При
проверке устойчивости получаемых решений
обнаруживается зона неустойчивых колебаний,
диапазон частот которых
) (кривая 1 на рис. 1) только
количественно отличается от соответствующей зависимости,
описывающей вынужденные колебания ПС [10] . При
проверке устойчивости получаемых решений
обнаруживается зона неустойчивых колебаний,
диапазон частот которых 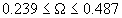 превышает размеры зоны
неоднозначности, характерной для систем со
скачкообразным резонансом. Согласно результатам
численного эксперимента возбуждение
неустойчивых колебаний, вызванных пульсацией
купола, сопровождается сменой режима "малых"
несимметричных колебаний, совершаемых
относительно установившегося спуска ПС с углом
атаки
превышает размеры зоны
неоднозначности, характерной для систем со
скачкообразным резонансом. Согласно результатам
численного эксперимента возбуждение
неустойчивых колебаний, вызванных пульсацией
купола, сопровождается сменой режима "малых"
несимметричных колебаний, совершаемых
относительно установившегося спуска ПС с углом
атаки 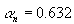 , режимом "больших" симметричных
колебаний, совершаемых относительно
вертикального спуска с нулевым углом атаки.
, режимом "больших" симметричных
колебаний, совершаемых относительно
вертикального спуска с нулевым углом атаки.
При а = 0.2 в диапазоне частот 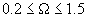 решения,
соответствующие вещественным положительным
значениям амплитуды А52,
отсутствуют. Это означает, что в указанном
диапазоне частот пульсация купола нелинейной
модели ПС не может служить причиной возбуждения
субгармонических колебаний порядка 1/2. Решения ,
соответствующие вещественным положительным
значениям амплитуды А52,
находятся у нелинейной модели ПС при
решения,
соответствующие вещественным положительным
значениям амплитуды А52,
отсутствуют. Это означает, что в указанном
диапазоне частот пульсация купола нелинейной
модели ПС не может служить причиной возбуждения
субгармонических колебаний порядка 1/2. Решения ,
соответствующие вещественным положительным
значениям амплитуды А52,
находятся у нелинейной модели ПС при 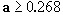 . При этом
в диапазоне частот существования
субгармонических колебаний, возбуждаемых
пульсацией купола, образуется зона неустойчивых
расходящихся колебаний. Кривая зависимости
. При этом
в диапазоне частот существования
субгармонических колебаний, возбуждаемых
пульсацией купола, образуется зона неустойчивых
расходящихся колебаний. Кривая зависимости 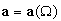 ,
отделяющая эту зону от зоны устойчивых
гармонических и субгармонических (порядка 1/2)
колебаний, построена на рис. 2.
,
отделяющая эту зону от зоны устойчивых
гармонических и субгармонических (порядка 1/2)
колебаний, построена на рис. 2.
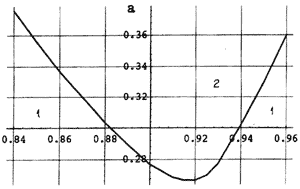
Рис.2. Граница области устойчивых колебаний ПС,
вызванных пульсацией купола.
1. Устойчивые колебания.2. Неустойчивые
колебания.
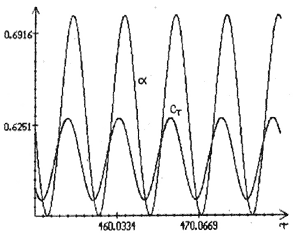
Зависимости 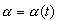 , построенные по
результатам численного интегрирования
уравнений (1) при различных значениях а и
, построенные по
результатам численного интегрирования
уравнений (1) при различных значениях а и 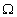 диапазона
частот существования субгармонических
колебаний порядка 1/2, представлены на рис.3.
диапазона
частот существования субгармонических
колебаний порядка 1/2, представлены на рис.3.
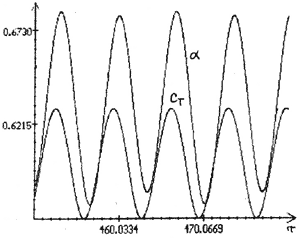 а = 0.2 |
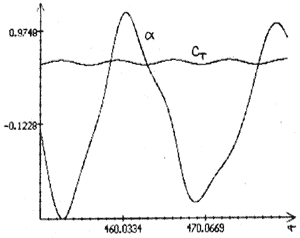 а = 0.34 |
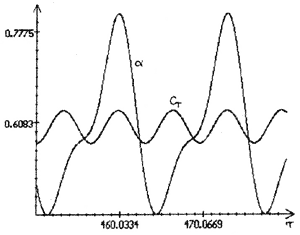
Рис.3a. Зависимости  , построенные по
результатам
, построенные по
результатам
интегрирования уравнений (2) при 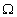 = 0.92.
= 0.92.
  = 0.96 = 0.96 |
 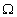 = 1.0 = 1.0 |
Рис.3б. Зависимости 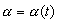 ,
построенные по результатам
,
построенные по результатам
интегрирования уравнений (2) при а = 0.32.
Кривая 2 на рис. 1 соответствует
зависимости А51=А51(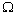 ) линейной модели ПС,
у которой коэффициент CN
аппроксимируется функцией
) линейной модели ПС,
у которой коэффициент CN
аппроксимируется функцией
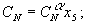 где
где 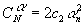 .
.
Здесь, как и в случае нелинейной модели
ПС, при а = 0.2 в диапазоне частот 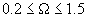 искомые
периодические решения с вещественными
положительными значениями амплитуды А52 отсутствуют. Отсутствуют такие
решения и при
искомые
периодические решения с вещественными
положительными значениями амплитуды А52 отсутствуют. Отсутствуют такие
решения и при 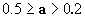 ; т. е. при значениях а, допустимых
с физической точки зрения, пульсация купола
может вызывать колебания линейной модели ПС
только с частотой пульсации
; т. е. при значениях а, допустимых
с физической точки зрения, пульсация купола
может вызывать колебания линейной модели ПС
только с частотой пульсации 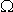 .
.
До сих пор предполагалось, что
невозмущенным движением ПС является
установившееся снижение с углом атаки 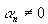 , -
движение, характерное для ПС, у которой ткань
купола имеет малую проницаемость. Для ПС с тканью
купола большой проницаемости система (3)
вырождается в следующую
, -
движение, характерное для ПС, у которой ткань
купола имеет малую проницаемость. Для ПС с тканью
купола большой проницаемости система (3)
вырождается в следующую
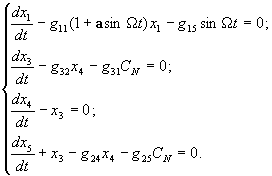 (12)
(12)
Как видно, слагаемые, которые характеризуют пульсацию купола, входят только в первое уравнение системы (12), изолированное от остальных уравнений системы. Это означает, что та пульсация купола, о которой шла речь выше, на движение ПС, имеющей ткань купола большой проницаемости, заметного влияния не оказывает. Этот вывод подтверждается результатами численного интегрирования системы (1).
Список литературы
Сведения об авторах
Чуркин Валерий Михайлович, профессор кафедры теоретической механики Московского государственного авиационного института (технического университета), д.ф.-м.н.,
Попов Дмитрий Александрович, аспирант кафедры теоретической механики Московского государственного авиационного института (технического университета).
Серпичева Елена Викторовна, старший преподаватель кафедры машиноведения и деталей машин Московского государственного авиационного института (технического университета).