11. Примеры самоорганизации

Рассмотрим в качестве примера макроскопическую неустойчивость Бернара [7] . Речь идет о следующей системе. В тонком слое жидкости поддерживается разность температур между нижней, подогреваемой, поверхностью и верхней поверхностью, которая находится при комнатной температуре. При малой разности температур перенос тепла осуществляется за счет теплопроводности. Выше определенного порога разности температур тепло переносится за счет конвекции, т.е. молекулы участвуют в коллективных движениях, соответствующих вихрям, разделяющим слой жидкости на регулярные ячейки - вихри Бернара.

Предсказать конкретный результат самоорганизации первоначально однородной системы невозможно. Говорят, что вихри Бернара образуются случайно при росте флюктуаций вследствие положительных обратных связей. Так же случайно происходит выпадение орла или решки при подбрасывании монеты. Так же случайна самоорганизация атомов в простейшие молекулы ДНК, которая привела к жизни.

Уменьшение энтропии макро состояния вследствие хаотического поведения микросостояния необратимо, как и обычное увеличение энтропии, потому что хаотическое поведение всегда необратимо уже в силу гиперчувствительности к начальному состоянию, независимо от того, обратимы или необратимы во времени элементарные законы поведения компонентов макросистемы. Если изменить скорости всех молекул на противоположные, вихри Бернара все равно будут образовываться из флюктуаций. Так что "стрела времени", т.е. выделенное направление хода времени, т.е. необратимость времени, является простым следствием гиперчувствительности.

Макроскопическая самоорганизация не обязательно требует контакта с внешней средой, как это имело место в случае вихрей Бернара. Изолированная смесь водорода и кислорода может постепенно, даже без взрыва, самоорганизоваться в воду. Однородный первоначально газ за счет самогравитации может распасться на отдельные сгустки, если гравитационная энергия, выделяющаяся при образовании флюктуаций плотности, превысит кинетическую энергию хаотического теплового движения. Возможно, этот процесс привел к образованию галактик и звезд во Вселенной.

Примером макроскопической самоорганизации может служить естественный отбор. Пример отбора, причем даже не естественного отбора, а случайного отбора, дал в виде простой игры Манфред Эйген [6] . В игровой ящик кладут N различных пронумерованных шаров. Кроме того, имеется запас шаров, в котором каждый номер представлен N шарами. При игре из ящика достают случайно выбранный шар и либо удаляют его вообще, либо удваивают, то есть кладут обратно в ящик, добавив второй шар с тем же номером из запаса. Если удаление и удваивание шаров чередовать, то число шаров в ящике будет сохраняться, однако, в конце концов, там окажутся шары только одного какого-то номера. Все остальные номера "вымрут". Причем никак нельзя предугадать заранее, какой номер победит.

12. Квантовомеханическая неопределенность

Квантовый мир, лежащий буквально у нас под носом, бросил человеческому интеллекту неотразимый вызов [8] . Чтобы разъяснить ситуацию, заметим сначала, что для расчета, например угла разлета бильярдных шаров, необходимо обработать не очень много информации. Опытный человек хорошо с этим справляется. Но если радиус шаров значительно уменьшить, та же точность расчета угла разлета потребует значительно большего объема информации, более точного определения координат и направления скорости шаров, потому что маленькие шарики гораздо чувствительнее больших к изменению их координат и направления скорости. Так вот оказалось, что природа не допускает бесконечного возрастания точности и объема информации, связанных с уменьшением размера частицы. Природа позволяет определять или задавать координаты и импульсы частиц лишь с некоторой неопределенностью. Произведение минимальных значений этих неопределенностей равно постоянной Планка h,

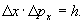
Возможно, это обстоятельство связано с тем, что природе вообще чуждо понятие бесконечности. Придуманное интеллектом человека, склонным к абстрактному мышлению, это понятие может быть не адекватно природе.

Математически неопределенность координат и скоростей частиц проявляется в том, что состояние микроскопической частицы описывается не ее координатой и импульсом, как в классической физике, а так называемой волновой функцией, которая выражает размазанность частицы в нашем пространстве и в пространстве импульсов. Например, если c помощью светофильтров мы допускаем к нам только монохроматические фотоны, то импульс каждого фотона будет известен с небольшой погрешностью, 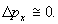Зато координата фотона, а, значит, и время прилета почти совсем неопределенны, 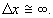В соответствии с этим волновая функция монохроматического фотона

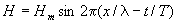
размазана по всему нашему пространству, но в пространстве импульсов она сконцентрирована вблизи точки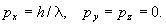

Если на пути нашего фотона расположен экран, фотопластинка, то фотон будет захвачен одним из атомов, который из-за этого превратится в ион за счет фотоэффекта. При этом неопределенность координаты фотона резко уменьшится. Она сделается порядка размера атома, зато возникнет значительная неопределенность импульса, рассматриваемого как вектор. Говорят, что волновая функция редуцировала. Если при этом за фотопластинкой не велось наблюдение, можно сказать, что квантовомеханическая неопределенность сменилась человеческой неосведомленностью.

Захваченный фотон запустит химическую реакцию, которая изменит цвет небольшой области. Можно приготовить усилитель, который это изменение усилит, так что в момент захвата загорится контрольная лампочка, и мы будем уведомлены о захвате фотона.

Следует знать, однако, что Э. Шредингер предложил в 1935 году знаменитый мысленный эксперимент, в котором наш усилитель не лампочку зажигает, а разбивает бутылку с цианистым калием и тем самым убивает кошку, сидящую в закрытой коробке. Шредингер утверждал, что, поскольку принципиально не определено, какой атом и когда захватит электрон, столь же принципиально не определен вопрос о жизни или смерти кошки. Другими словами, кошка находится между жизнью и смертью до тех пор, пока не будет подвергнута прямому наблюдению, что, конечно, парадоксально. На наш взгляд, Э. Шредингер неоправданно смешивал неопределенность и неосведомленность.

13. Волновая функция. Пространственное распределение квантовых частиц

Состояние квантовой частицы описывается не координатами и импульсом, которые объективно не известны, а волновой функцией [9]

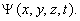
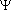- волны для частиц были предложены Луи де Бройлем в 1924. Волновая функция показывает, как состояние частицы "размазано" по фазовому пространству. Она позволяет, в частности, вычислить вероятность dP зарегистрировать частицу в элементе объема dxdydz, независимо от импульса:

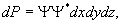
или вычислить среднее значение какой-нибудь координаты, например, x :

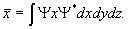
Здесь 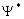- комплексно сопряженная волновая функция. Такую интерпретацию волновой функции дал Макс Борн в 1926 году. Таким образом, квадрат модуля, 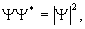волновой функции можно рассматривать как плотность вероятности или как пропорциональную ей плотность частиц 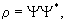то есть как функцию распределения в пространстве.

Для того чтобы привести пример волновой функции, рассмотрим электрон, ускоренный определенной разностью потенциалов и летящий вдоль оси x. Энергия E и импульс p такого электрона определены. Однако, в соответствии с соотношением неопределенности, координата его не определена. Поэтому состояние электрона изображается не точкой в фазовом 6-пространстве 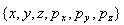, а плоскостью

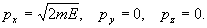
Согласно идее де Бройля, состояние такого электрона в реальном пространстве описывается

комплексной волной, у которой частота и длина волны могут быть найдены по формулам, относящимся к фотонам,

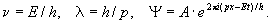
Для такой волновой функции 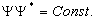Это и означает, что электрон равномерно размазан по нашему пространству.

В общем случае 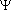- волны подчиняются не волновому уравнению, а уравнению, полученному Эрвином Шредингером в 1925 году:

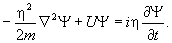
Здесь 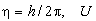- потенциальная энергия частицы, i - мнимая единица.

Для того чтобы рассмотреть частицу, локализованную в некоторой области пространства, надо использовать в качестве ее волновой функции не бесконечную гармоническую волну де-Бройля, а волновой пакет произвольной формы, например, с гауссовой огибающей, имеющей некоторую характерную длину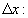

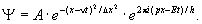
Такая волновая функция не является монохроматической. Она содержит гармонические составляющие, расположенные вблизи волны де-Бройля 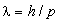в интервале длин волн порядка

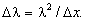
Это означает, что импульс такой частицы определен с погрешностью

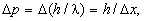
и ее состояние в фазовом пространстве {x,p} изображается областью размером

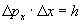
в соответствии с соотношением неопределенности. При локализации частицы по всем трем координатам она будет занимать в фазовом 6-пространстве объем

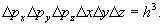
Этот объем называется фазовой ячейкой.