14. Корпускулярная и континуальная концепция описания природы

Предположим, что пулемет обстреливает броневой щит с двумя близко расположенными отверстиями ╧1 и ╧2, так что часть пуль пролетает сквозь эти отверстия и попадает на экран, который мы будем рассматривать как наблюдательный [8] . Пролетающие через отверстия пули сильно рассеиваются и поэтому довольно равномерно покрывают значительную площадь экрана. Очевидно, что если I₁ - плотность потока пуль в некоторой точке экрана, проходящих через отверстие ╧1 (при закрытом отверстии ╧2), а I₂ - плотность потока пуль в той же точке экрана, проходящих через отверстие ╧2 (при закрытом отверстии ╧1), то плотность потока пуль через оба отверстия будет равна

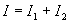
Таков закон сложения двух потоков частиц или корпускул. Кроме того, в принципе возможен точный расчет траектории полета и места попадания на экран любой пули.

Рассмотрим теперь вместо пулемета источник волн на поверхности моря. Эти волны распространяются вплоть до заградительного ряда из барж, между которыми оставлены два близко расположенных прохода, проход ╧1 и проход ╧2. Волны, прошедшие через эти проходы, в конце концов, достигают наблюдательного экрана.

Рассматриваемые волны характеризуются отклонением H поверхности воды от равновесного уровня. H является функцией координат и времени и аналогична волновой функции квантовой механики. Она представляет собой бегущую волну, например, синусоидального вида:

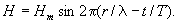
Здесь r - расстояние до прохода, 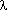- длина волны, T - период колебаний.

Распространение волн, однако, значительно отличается от полета пуль. Во-первых, волновая функция H принимает отрицательные значения, потому что уровень воды отклоняется то вверх, то вниз. Во-вторых, плотность потока энергии волн зависит от квадрата волновой функции:

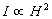
В-третьих, нельзя говорить, что волна прошла от источника до экрана либо через проход ╧1, либо через проход ╧2, как это было в случае пуль, волна использует оба прохода. Если закрыть один из проходов, волнение перед экраном изменится качественно, а не просто уменьшится вдвое, как в случае пуль. Волнение H₁, возникающее, если открыт только проход ╧1, складывается с волнением H₂, возникающим, если открыт только проход ╧2:

H = H₁ + H₂

Это называется суперпозицией. При этом образуются зоны, где суммарная волновая функция равна нулю:

H = H₁ + H₂ = 0

Это зоны спокойной воды, где отсутствует волнение, где одна волна погасила другую. Такое явление называется интерференцией. При интерференции складываются волновые функции, а не плотности потоков. Результирующая плотность потока может быть вычислена как квадрат суммарной волновой функции:

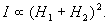
В частности, плотность потока равна нулю в зонах, где отсутствует волнение.

15. Интерференция света при квантовом рассмотрении

Электромагнитные волны, которые мы для краткости будем называть светом, на первый взгляд, похожи на морские волны. Мы снова рассмотрим конструкцию того же типа: источник освещает непрозрачный экран с двумя близко расположенными отверстиями, ╧1 и ╧2, за которым находится наблюдательный экран. На этом экране наблюдается интерференционная картина. Однако при уменьшении интенсивности света становится очевидно, что интерференционная картина распадается на отдельные вспышки. Если наблюдательный экран покрыт светочувствительным слоем, он постепенно покроется черными фотографическими зернами. Это происходит потому, что свет распространяется и поглощается порциями. Эти порции называются квантами света или фотонами. Атомы светочувствительного слоя, захватывая порции света, возбуждаются и при проявлении становятся зародышами фотографических зерен.

Квантование света использовал Планк, занимаясь тепловым излучением и доказал Эйнштейн, объяснив фотоэффект. Энергия фотонов равна

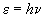
а импульс фотонов

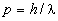
h = 6,6·10^-34 Дж·с - постоянная Планка, - частота света, 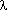- длина волны.

Задолго до Эйнштейна, во времена торжества волновой теории света, только Ньютон с прозорливостью гения последовательно отстаивал корпускулярную теорию света, несмотря на полную невозможность совместить ее с результатами интерференционных опытов. Интерференция фотонов действительно не может быть объяснена в том смысле, что не существует аналогичного явления в знакомом нам макроскопическом мире вещей.

Если закрыть отверстие ╧2, интерференционная картина исчезнет. Магнитная составляющая H электромагнитной световой волны, прошедшей через отверстие ╧1, сделается примерно одинаковой в различных точках экрана. Соответственно, экран будет равномерно покрываться фотографическими зернами. В этом не было бы ничего удивительного. Однако после открывания отверстия ╧2 фотоны перестанут попадать в те места, где суммарная волновая функция H = H₁ + H₂ = 0, несмотря на то, что отверстие ╧1 по-прежнему остается открытым. Невозможно понять, каким образом фотоны могут гасить фотоны.

Однако самые удивительные явления возникают, если свет заменить потоком электронов [8] . Оказывается, электроны создают примерно такую же интерференционную картину, как фотоны. Другими словами, электроны, как и фотоны, могут интерферировать друг с другом, в частности, гасить друг друга. Больше того, выяснилось, что все элементарные частицы ведут себя подобным удивительным образом. Для того чтобы рассчитывать подобные явления ученые и создали квантовую механику.

16. Вещество и поле. Принцип Паули

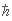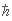Материя представлена в мире двумя типами: вещество и поле [9] . Материя обоих типов квантована, то есть, разбита на порции. При этом кванты могут вращаться вокруг своей оси. Соответствующий момент количества движения кванта называется спином s. Единицей измерения спина служит величина . Кванты вещества, то есть частицы, имеют полуцелый спин: s/ = 1/2, 3/2,..., и, в свою очередь, разбиты на два типа: 1) легкие или лептоны (электроны, позитроны, нейтрино, мюоны), 2) тяжелые или барионы (протоны, нейтроны, гипероны). Кванты поля, иногда тоже называемые частицами, имеют целый спин, s/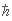 = 0, 1, 2,... Это глюоны, мезоны и электромагнитные кванты с энергией h.

Внутренняя структура лептонов неизвестна, а барионы и некоторые мезоны состоят из кварков, которые являются частицами вещества. Нейтроны n и протоны p состоят из троек кварков: 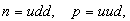а - мезон √ из кварка и антикварка: 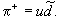Заряды u-кварка и d-кварка равны соответственно +2/3 и -1/3 заряда электрона. Заряды антикварков противоположны по знаку.

Частицы с полуцелым спином подчиняются запрету Паули: все они должны отличаться друг от друга состоянием.

Взаимное притяжение трех кварков друг к другу можно для наглядности объяснить, приписав кваркам "цвета", например, красный, желтый, синий, имея в виду, что нейтральная цветовая комбинация, получающаяся при сложении этих цветов, имеет наименьшую потенциальную энергию так же, как наименьшую энергию имеет нейтральная комбинация электрических зарядов в электродинамике. Антикваркам приписываются дополнительные цвета: оранжевый, зеленый, фиолетовый.

17. Распределения Максвелла-Больцмана и Ферми-Дирака

Точки, изображающие состояния классических частиц в фазовом 6-пространстве, распределены по этому пространству не равномерно, а согласно распределению Максвелла-Больцмана [2] . Вероятное количество точек в элементе dxdydzdp_xdp_ydp_z , пропорциональное вероятности найти частицу в состоянии, соответствующем этому элементу, равно

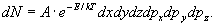
Здесь 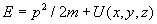- сумма кинетической и потенциальной энергии частицы в этом состоянии, A - нормировочная постоянная, Дж/К √ постоянная Больцмана, T - температура. При T = 0 все частицы покоятся там, где потенциальная энергия минимальна.

При совместном рассмотрении N электронов, находящихся, например, в куске металла объемом V, надо учитывать, что каждую ячейку фазового пространства размером h³ может занимать только одна пара электронов со спинами противоположной ориентации [9] . Поэтому, в отличие от молекул газа, электроны не могут при T = 0 все оказаться в состоянии с E = 0, как следует из распределения Максвелла-Больцмана. Их фазовые ячейки занимают все положения с возможно меньшей энергией, заполняя, в первом приближении, шар такого радиуса в импульсном пространстве, чтобы в нем как раз поместились ячейки всех N электронов. Радиус этого шара, p_m,определяется из соотношения:

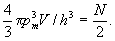
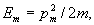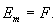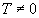Это значит, что при T = 0 электроны занимают все возможные энергетические уровни от нулевого до максимального, который называется энергией Ферми Для реальных металлов энергия Ферми весьма велика, по сравнению с энергией теплового движения при комнатной температуре. Поэтому при тепловую энергию получают электроны, занимающие в фазовом пространстве тонкий слой вблизи F. Распределение электронов в металле получено Ферми и Дираком. Оно заменяет распределение Максвелла-Больцмана и выглядит:

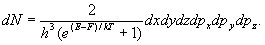
Поэтому частицы вещества называются фермионы.

18. Связанное состояние фотонов

Сравнительно недавно ученые научились, используя нелинейные кристаллы, уменьшать частоту электромагнитных волн вдвое. С квантовой точки зрения фотоны при этом разделялись на две равные части. При этом направления полета фотонов и их поляризация оставались в большой степени неопределенными. Однако, по закону сохранения импульса, направление полета одного из этих фотонов определяло направление другого. Точно так же поляризации этих фотонов оказывались связанными друг с другом.

Связанные состояния квантовых частиц давно рассматриваются учеными, потому что с ними связан квантовомеханический парадокс, придуманный в 1935 году А. Эйнштейном, Б. Подольским, Н. Розеном. В оригинале в этом парадоксе фигурируют не фотоны, а протоны. Однако в последнее время именно на фотонах демонстрируются различные варианты этого парадокса.

Пусть два связанных фотона разлетаются по закону сохранения импульса в противоположных направлениях. При этом из-за того, что энергия и импульс фотонов известны с высокой точностью, их радиальные координаты и момент времени разлета не определены. Момент импульса фотонов точно равен нулю. Поэтому не определена угловая координата фотонов. Другими словами, не определено направление, вдоль которого они разлетаются в разные стороны. Важно понимать, что не определено √ это значит, сами фотоны не знают, как они летят. Направление разлета выясняется только при регистрации одного из фотонов. А это может произойти через десятки тысяч лет на краю Галактики. Тем не менее, второй фотон должен быть зарегистрирован на другом краю Галактики на строго противоположном направлении. Каким образом второй фотон, направление полета которого объективно не определено до момента регистрации первого, может узнать, на каком направлении ему следует зарегистрироваться, это уму непостижимо! Но природа каким-то образом умудряется соблюдать одновременно и закон сохранения импульса, и запрет теории относительности на передачу сигналов со сверхсветовой скоростью, и законы формальной логики, и ограничение на объем информации! Эйнштейн отметил, что такое поведение природы нельзя сопоставить ни с какой "реалистической" моделью из обыденной действительности. Возможно, это глубокое замечание Эйнштейна как раз и означает, что люди не в состоянии понять квантовую механику.