УДК 681.31
Нейросетевая система как метод решения задачи идентификации состояния сложного технического объекта
Н.Ю. Ященко, Е.М. Будкина
В настоящей работе обсуждаются нейро-нечеткие методы для построения системы ситуационного управления поведением сложного технического объекта на основе текущей информации.
Современные технические объекты, к которым относятся в частности транспортные средства, приближаются к уровню сложности, при котором их поведение и свойства не являются суммой свойств отдельных компонент [1] . Под сложными объектами будем понимать системы, в которых при вычленении компонент могут быть потеряны принципиальные свойства, а при добавлении компонент возникают качественно новые свойства. Каждая из компонент системы может быть описана набором характеристических признаков, значения которых определяют текущее состояние компонента и системы в целом. Таким образом, поведение системы описывается вектором значений характеристических признаков с учетом влияния внешних факторов на поведение системы.
Задача управления сводится к построению решающего правила, позволяющего осуществлять контроль и диагностику работоспособности системы. При этом необходимо учитывать большой объем трудноформализуемых параметров сложной технической системы, который необходимо обрабатывать в реальном масштабе времени.
Предлагается для построения решения по управлению использовать парадигму ситуационного управления, которая заключается в отнесении текущей ситуации с некоторым значением функции принадлежности к некоему классу (штатных или нештатных ситуаций), которому ставится в соответствие решение по управлению.
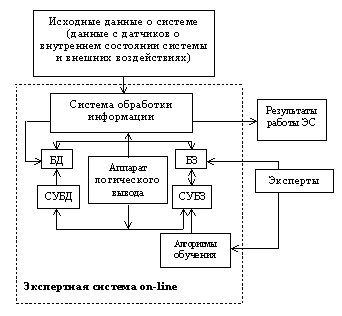
Экспертная система on-line на основе нейро-нечеткой парадигмы
Система поддержки принятия решений по управлению транспортным средством как сложной технической системой основывается на создании экспертной системы (ЭС) функционирующей в реальном масштабе времени (on-line). Структура такой системы приведена на рисунке 1. База данных (БД) содержит информацию о текущем состоянии объекта. В базе знаний (БЗ) находятся понятия конкретной предметной области, а также экспертные знания. Аппарат логического вывода координирует процессы ЭС, используя системы управления БД (СУБД) и БЗ (СУБЗ), принимает решения по управлению сложным техническим объектом.
ЭС on-line должна отслеживать большой поток быстро меняющихся параметров, принимать качественные и своевременные решения по управлению технической системой [2] .
Так как управлению должно проводиться в реальном масштабе времени, предполагается наличие математического аппарата, позволяющего обрабатывать большой поток сложноструктурированной информации о текущем состоянии технической системы. Основу такого математического аппарата составляют алгоритмы глобального распараллеливания вычислительных процессов. К таким моделям относятся искусственные нейронные сети (НС).
Сложность технической системы, содержание в датчиках погрешностей, неизмеряемость части параметров, возможность комплексного отказа датчиков, отсутствие точной математической модели является основанием для применения в экспертной системе аппарата нечетких множеств (НМ).
ЭС on-line с использованием НС и НМ может применяться на стендовых испытаниях и в эксплуатационном режиме.

Рис. 1. Функциональная схема экспертной системы on-line
Постановка задачи
В общем случае математическая модель сложной технической системы представляется функциональной зависимостью между переменными состояния системы, управляющими воздействиями, наблюдаемыми параметрами системы и внешней среды:
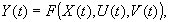 (1)
(1)
где 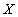 - вектор текущего состояния модели
системы,
- вектор текущего состояния модели
системы, 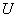 - вектор управляющих воздействий,
- вектор управляющих воздействий, 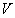 - вектор
внешних воздействий,
- вектор
внешних воздействий, 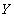 - вектор выходных сигналов
модели.
- вектор выходных сигналов
модели.
Необходимо разработать математическую модель функционирования сложной технической системы требующей наличие следующих данных о системе [3] :
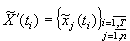 -
вектор характеристических признаков состояния
системы в момент времени
-
вектор характеристических признаков состояния
системы в момент времени 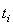 ;
;
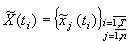 -
вектор ситуационных признаков состояния системы
в момент времени
-
вектор ситуационных признаков состояния системы
в момент времени 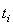 ;
;
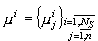 -
вектор степени влияния
-
вектор степени влияния 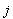 -го признака на
-го признака на 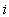 -ю
ситуацию;
-ю
ситуацию;
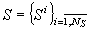 -
множество возможных ситуаций системы;
-
множество возможных ситуаций системы;
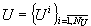 -
множество решений по управлению для перевода
системы из ситуации
-
множество решений по управлению для перевода
системы из ситуации 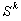 в ситуацию
в ситуацию 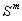 ,
,
где 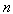 - число ситуационных признаков;
- число ситуационных признаков;
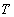 -
число векторов ситуационных признаков системы,
соответствующие дискретным моментам времени;
-
число векторов ситуационных признаков системы,
соответствующие дискретным моментам времени;
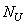 -
число решений по управлению;
-
число решений по управлению;
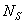 -
число возможных ситуаций системы.
-
число возможных ситуаций системы.
Вектор признаков 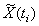 , характеризующий состояние системы
в ситуации
, характеризующий состояние системы
в ситуации 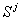
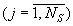 представим следующим образом:
представим следующим образом:
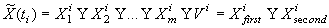 , (2)
, (2)
где 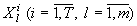 - набор признаков, характеризующих l -ую компоненту сложной системы, при
этом
- набор признаков, характеризующих l -ую компоненту сложной системы, при
этом 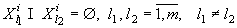 ,
, 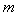 - число
выделенных компонент;
- число
выделенных компонент; 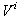 - вектор внешних
воздействий системы,
- вектор внешних
воздействий системы, 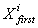 - набор первостепенных
ситуационных признаков,
- набор первостепенных
ситуационных признаков, 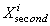 - набор второстепенных
ситуационных признаков, в общем случае
- набор второстепенных
ситуационных признаков, в общем случае 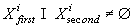 .
.
Целью работы является разработка методов построения системы ситуационного управления поведением сложной технической системы на основе текущей информации.
Задача решается при следующих ограничениях:
Представим множество всех ситуаций 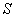 следующим образом:
следующим образом:
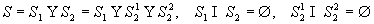 , (3)
, (3)
где 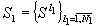 - множество штатных ситуаций;
- множество штатных ситуаций;
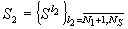 - множество нештатных ситуаций;
- множество нештатных ситуаций;
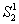 -
множество нештатных ситуаций, для которых
известны решения по управлению;
-
множество нештатных ситуаций, для которых
известны решения по управлению;
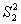 -
множество нештатных ситуаций, для которых
решения по управлению не известны.
-
множество нештатных ситуаций, для которых
решения по управлению не известны.
Таким образом, решение по переводу системы из одной ситуации в другую должны приниматься в следующих случаях:
1) 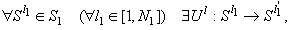
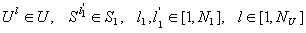 , т.е.
для любой штатной ситуации существует
соответствующее ей решение по управлению,
переводящее систему в другую штатную ситуацию;
, т.е.
для любой штатной ситуации существует
соответствующее ей решение по управлению,
переводящее систему в другую штатную ситуацию;
2) 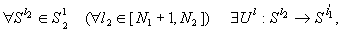
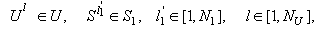 т.е.
для любой нештатной ситуации из множества
т.е.
для любой нештатной ситуации из множества 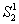 существует
соответствующее ей решение по управлению,
переводящее систему в штатную ситуацию если это
возможно, иначе принимается решение по
приостановке функционирования системы;
существует
соответствующее ей решение по управлению,
переводящее систему в штатную ситуацию если это
возможно, иначе принимается решение по
приостановке функционирования системы;
3) 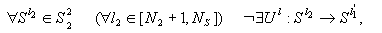
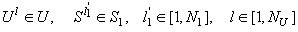 , т.е.
для любой нештатной ситуации из множества
, т.е.
для любой нештатной ситуации из множества 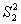 не
существует соответствующего ей решения по
управлению.
не
существует соответствующего ей решения по
управлению.
В первых двух случаях достаточно решить задачу
отнесения текущей ситуации к некоторому классу
ситуаций, для которых уже известно решение по
управлению. В третьем случае, когда не имеется
решения по управлению, необходимо сформировать
процедуру вывода решающего правила по переводу
системы из ситуации 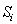 в ситуацию
в ситуацию 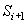 .
.
Нейросетевое моделирование
В качестве машины логического вывода предлагается использовать нейросетевую парадигму.
Основным принципом нейросетевого моделирования является принцип "черного ящика". В противоположность аналитическому подходу, при котором моделируется внутренняя структура системы, в данном случае моделируется внешнее функционирование системы. Функционирование системы в рамках такой модели описывается информационно, на основе данных экспериментов или наблюдений над реальной системой. Как правило, подобные модели проигрывают формальным математическим моделям и экспертным системам по степени "объяснимости" выдаваемых результатов, однако отсутствие ограничений на сложность моделируемых систем определяет их важную практическую значимость.
НС - это параллельная система обработки информации, состоящая из обрабатывающих элементов (нейронов), которые локально выполняют операции над поступающими сигналами и могут обладать локальной памятью.
Нейрон имеет n входных полюсов, на которые поступают входные сигналы x1,x2, ┘,xn от других нейронов или внешних источников. Входным сигналам приписаны веса w1, w2,┘,wn. Входная функция s нейрона задается взвешенной формой входных сигналов. Активационная функция f преобразовывает текущее состояние нейрона в выходной сигнал y согласно некоторому нелинейному закону, тогда функционирование нейрона будет выражаться формулой:
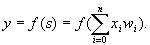 (4)
(4)
Из отдельных нейронов строятся НС различных архитектур. Наиболее распространенной является многослойная нейронная сеть прямого распространения. Такая НС состоит из слоя входных узлов, скрытых слоев и выходного слоя, соединенных последовательно в прямом направлении и не содержащих связи между нейронами внутри каждого слоя и обратных связей между слоями. Вход нейронной сети можно рассматривать как выход "нулевого слоя" вырожденных нейронов. Каждый выходной сигнал i -го слоя подается на вход всех нейронов (i+1)-го слоя. Выходом НС считается выход нейронов последнего слоя. Нейроны каждого слоя, в общем виде, могут иметь различные функции активации.
В процессе функционирования такая НС формирует выходной сигнал Xk в соответствии с входным сигналом Х0 по рекуррентной формуле:
Xk = fk(Wk-1Т · Xk-1) = fk(Wk-1Т · fk-1(Wk-2Т ·...· f1(W0Т · X0)...)) (5)
где k - число слоев в
сети; Хi - выход
нейронов i -го слоя; Х0
- вход сети; Wi - матрица весовых коэффициентов
между нейронами (i-1) и
iслоев; fi - активационная функция нейронов i -го слоя, 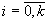 ,
, 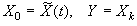 .
.
Таким образом, НС вычисляет линейные функции
многих переменных s,
нелинейные функции одного переменного f, а также суперпозиции функций
одного переменного при последовательном
соединении слоев. В процессе прохождения сигнала
по связям сети происходит его обработка,
результатом которой является выходной сигнал. НС
выполняет функциональное соответствие между
входом и выходом, и может служить информационной
моделью 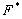 системы
системы 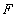 (1).
(1).
При моделировании реальных сложных
технических систем, значения системной функции F получаются на основе экспериментов
или наблюдений, которые проводятся лишь для
конечного набора параметров X. При этом значения как Y так и Х измеряются приближенно,
и подвержены ошибкам различной природы. Целью
моделирования является получение значений
системных откликов при произвольном изменении X. В этой ситуации может быть
применена информационная модель 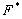 исследуемой системы F.
исследуемой системы F.
Задача идентификации текущего состояния системы могут быть отнесены к задачам распознавания. Существуют различные архитектуры НС выполняющие распознавание. Так как при создании модели сложной системы на основе экспериментальных данных не возможно учесть все ситуации системы, следовательно, при эксплуатации системы возникает неоднозначность классификации ситуаций, что приводит к использованию нечетких множеств.
Для построения информационной модели сложной технической системы, потребуется многоуровневая гибридная НС состоящая из подсетей различных архитектур. Рассмотрим построение НС для создания информационной модели отдельных компонент сложной технической системы.
Информационная модель компоненты сложного технического объекта
Предполагая, что множество всех ситуаций можно
условно разделить на множество штатных ситуаций 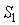 и
множество нештатных ситуаций
и
множество нештатных ситуаций 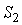 (2), необходимо по
результатам ограниченного числа измерений
(2), необходимо по
результатам ограниченного числа измерений  принять
адекватное решение по отнесению текущей
ситуации
принять
адекватное решение по отнесению текущей
ситуации 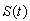 к одному из выше перечисленных
множеств. Решение задачи сводится к построению
решающего правила, осуществляющего необходимое
распознавание текущей ситуации с вычислением
значения функции принадлежности. Для решения
задачи в настоящей работе рассматривается
применение нейро-нечеткой НС.
к одному из выше перечисленных
множеств. Решение задачи сводится к построению
решающего правила, осуществляющего необходимое
распознавание текущей ситуации с вычислением
значения функции принадлежности. Для решения
задачи в настоящей работе рассматривается
применение нейро-нечеткой НС.
Будем предполагать, что система имеет четкие
входы и нечеткие степени влияния каждого входа
на ситуацию. Тогда построим двухуровневую
нечеткую НС, которая будет осуществлять контроль
за состоянием 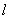 -ой
-ой 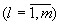 компоненты - "эксперт компоненты".
Первый уровень осуществляет предварительный
контроль состояния исходя из текущего значения
первостепенных ситуационных признаков
компоненты - "эксперт компоненты".
Первый уровень осуществляет предварительный
контроль состояния исходя из текущего значения
первостепенных ситуационных признаков 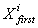 . Второй
уровень уточняет полученные значения, используя
для этой цели набор вторичных ситуационных
. Второй
уровень уточняет полученные значения, используя
для этой цели набор вторичных ситуационных 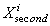 (2). Каждый
уровень реализуется НС, которая имеет следующие
характеристики (рис. 2):
(2). Каждый
уровень реализуется НС, которая имеет следующие
характеристики (рис. 2):
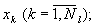 первый
слой осуществляет фильтрацию ситуационных
признаков
первый
слой осуществляет фильтрацию ситуационных
признаков 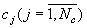 ; второй слой состоит из двух
нейронов выхода
; второй слой состоит из двух
нейронов выхода 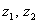 и осуществляет идентификацию
(первичную или вторичную) ситуации (штатная/нештатная);
и осуществляет идентификацию
(первичную или вторичную) ситуации (штатная/нештатная);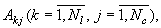
такие, что
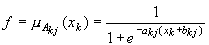 , (6)
, (6)
где 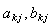 - настраеваемые в процессе обучения
параметры.
- настраеваемые в процессе обучения
параметры.
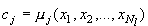 [4] ;
[4] ;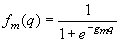 ; (7)
; (7)
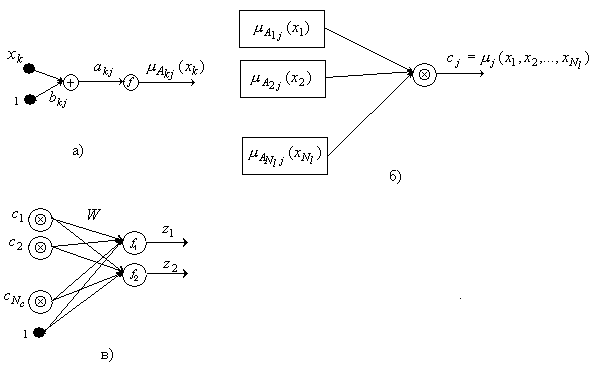
Рис. 2. Составные элементы НС √
"эксперт компоненты":
а) построение функции принадлежности для
признака 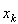 ситуации
ситуации 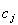 ;
;
б) архитектура одного нейроны второго слоя;
в) архитектура второго слоя.
Функционирование НС (5) для уровня принимаем вид:
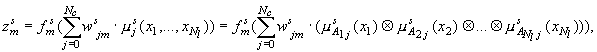 (8)
(8)
где 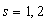 - номер уровня,
- номер уровня, 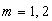 - выход уровня,
- выход уровня, 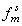 - функция
активации выходного слоя,
- функция
активации выходного слоя, 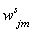 - элементы
транспонированной матрицы весовых
коэффициентов второго слоя
- элементы
транспонированной матрицы весовых
коэффициентов второго слоя 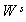 , размер матрицы
, размер матрицы 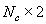 ,
, 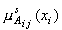 - функция принадлежности
входного параметра
- функция принадлежности
входного параметра 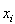 ситуационному признаку
ситуационному признаку 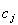 , знак
, знак 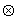 обозначает
операцию агрегирования.
обозначает
операцию агрегирования.
На этапе обучения происходит настройка параметров функций принадлежности первого слоя, весовых коэффициентов и параметра функции принадлежности второго слоя.
Принцип работы "эксперта-компоненты". На вход
первого уровня подаются первостепенные
параметры состояния компоненты, рассчитывается
выход НС. Если 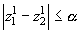 , т. е. нельзя однозначно определить
состояние компоненты, в этом случае подключается
НС второго уровня и результатом контроля
считается
, т. е. нельзя однозначно определить
состояние компоненты, в этом случае подключается
НС второго уровня и результатом контроля
считается 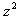 .
.
Предложенная НС в качестве машины вывода решений ЭС on-line позволяет применять вышеописанную ЭС для решения задач текущего контроля и диагностики как отдельных компонент системы так и свей системы в целом.
Список литературы
Сведения об авторах
Ященко Наталья Юрьевна, доцент кафедры дифференциальных уравнений Московского авиационного института (государственного технического университета), к.т.н.
E-mail: k803@mai.ru
Будкина Елена Михайловна, старший преподаватель кафедры математического с программного обеспечения вычислительных машин, систем, комплексов и сетей филиала "Восход" Московского авиационного института (государственного технического университета)
E-mail: lenok@baikonur.ru