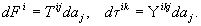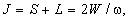УДК: 539.123.17
Внутренняя неполнота теории Максвелла
Р.И. Храпко
В 1999 году был предложен специфический
эксперимент, доказывающий, что неограниченная
плоская электромагнитная волна круговой
поляризации несет спиновый момент импульса,
вопреки общепринятому мнению. Показано, что
поглощение волны круговой поляризации
макроскопической мишенью не может быть описано в
рамках теории Максвелла, но требует
дополнительного введения классического тензора
спина электродинамики. Критикуется недавняя
публикация Аллена в "American J. of Physics" о поглощении луча круговой
поляризации.
Весной 1999 года на семинаре В. Л. Гинзбурга был
поднят важный, на мой взгляд, вопрос. Речь шла о
поглощении световой волны круговой поляризации
плоской круглой мишенью, разделенной узким
зазором на две концентрические части: внутренний
диск и внешнее кольцо. Вопрос о поведении такой
мишени содержится также в публикации [1] .
Проблема заключается в следующем. Согласно
распространенной точке зрения, плоская
неограниченная волна круговой поляризации не
несет момента импульса, поскольку вектора E и H всюду
перпендикулярны направлению распространения
волны, а вектор Пойнтинга, 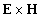 , и, соответственно,
плотность импульса направлены вдоль этого
направления [2 √ 8]. Однако на периферии реальной
световой волны с конечным поперечным сечением,
там, где интенсивность полей уменьшается,
существуют составляющие векторов E и H,
напрвленные вдоль распространения волны, а
, и, соответственно,
плотность импульса направлены вдоль этого
направления [2 √ 8]. Однако на периферии реальной
световой волны с конечным поперечным сечением,
там, где интенсивность полей уменьшается,
существуют составляющие векторов E и H,
напрвленные вдоль распространения волны, а 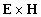 имеет
составляющую, перпендикулярную направлению
распространения. В результате, на периферии
световой волны, то есть на поверхности луча,
локализован момент импульса
имеет
составляющую, перпендикулярную направлению
распространения. В результате, на периферии
световой волны, то есть на поверхности луча,
локализован момент импульса
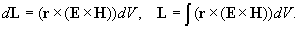
Я применяю здесь букву L,
обозначающую обычно орбитальный момент
импульса, однако научная общественность
рассматривает этот момент импульса как спин
луча.
Если такой луч поглощается мишенью, то мишень
получает момент импульса и закручивается, если
она свободно подвешена. Возникает однако вопрос,
вся мишень равномерно получает этот момент
импульса, или только ее внешняя часть, куда
падает поверхность луча, несущая, согласно
формуле, момент импульса?
По теории Максвелла, для определения силового
воздействия электромагнитного поля следует
использовать максвелловский тензор напряжений,
то есть пространственную часть тензора
энергии-импульса. Выражение 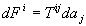 дает силу,
действующую на инфинитезимальную площадку
дает силу,
действующую на инфинитезимальную площадку 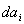 . Согласно
этому выражению, центральная часть мишени, на
которую падает внутренность луча, будет
испытывать световое давление и не будет
испытывать касательных сил, потому что поток
импульса в центральной части луча направлен
перпендикулярно мишени. Внешняя часть мишени, на
которую падает поверхность луча, будет
испытывать касательные силы, поскольку в районе
поверхности луча вектор Пойнтинга имеет
касательную к мишени составляющую. Эти
касательные силы и сообщают мишени упомянутый
момент импульса.
. Согласно
этому выражению, центральная часть мишени, на
которую падает внутренность луча, будет
испытывать световое давление и не будет
испытывать касательных сил, потому что поток
импульса в центральной части луча направлен
перпендикулярно мишени. Внешняя часть мишени, на
которую падает поверхность луча, будет
испытывать касательные силы, поскольку в районе
поверхности луча вектор Пойнтинга имеет
касательную к мишени составляющую. Эти
касательные силы и сообщают мишени упомянутый
момент импульса.
Из этого рассуждения следует, что если мишень
разделить узким зазором на две концентрические
части, внутренний диск и внешнее кольцо, то лишь
кольцо будет получать момент импульса и будет
закручиваться. Внутренний диск не будет получать
момент импульса и не будет закручиваться.
В то же время очевидно, что волна круговой
поляризации несет энергию и спиновый момент
импульса всегда в пропорции 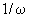 . Это означает, что
центральный диск мишени, получающий энергию и
световое давление, будет получать и спиновый
момент импульса, не описываемый теорией
Максвелла, и будет закручиваться, вопреки
вышеприведенному рассуждению. Такой вывод
следует и из простого рассуждения Р. Фейнмана,
который рассказывает, как световая волна
круговой поляризации передает вращающий момент
поглощающей среде [9] . Все это наводит на мысль,
что если мы хотим адекватно описывать
взаимодействие макроскопических предметов с
электромагнитным полем, нам следует расширить
теорию Максвелла, добавив к максвелловскому
тензору напряжений некий объект, описывающий
плотность крутящего воздействия.
. Это означает, что
центральный диск мишени, получающий энергию и
световое давление, будет получать и спиновый
момент импульса, не описываемый теорией
Максвелла, и будет закручиваться, вопреки
вышеприведенному рассуждению. Такой вывод
следует и из простого рассуждения Р. Фейнмана,
который рассказывает, как световая волна
круговой поляризации передает вращающий момент
поглощающей среде [9] . Все это наводит на мысль,
что если мы хотим адекватно описывать
взаимодействие макроскопических предметов с
электромагнитным полем, нам следует расширить
теорию Максвелла, добавив к максвелловскому
тензору напряжений некий объект, описывающий
плотность крутящего воздействия.
Обозначенное в предыдущем абзаце противоречие
сформулировано и в заметке [1] , отклики на которую
были недавно опубликованы [10, 11]. Аллен и Падгетт,
Юрченко согласны признать существование момента
импульса у плоской волны вопреки [2 √ 7]. Однако они
пытаются наделить плоскую волну спиновым
моментом импульса в рамках стандартной
электродинамики. Они пытаются объяснить
вращение диска в рамках стандартной
электродинамики. Авторы [10] пишут: "Любая форма
апертуры приводит к значительному градиенту
поля и порождает электромагнитные поля,
направленные вдоль луча. Так что проблема
потенциально разрешается."
Увы! Небольшой зазор между диском и кольцом не
апертуирует волну, не создает градиента, не
порождает продольного поля, не создает момента
импульса. Согласно стандартной электродинамике,
в районе диска отсутствуют пондеромоторные силы,
которые могли бы привести к закручиванию диска.
Максвелловские напряжения не способны привести
диск во вращение. Согласно стандартной
электродинамике, диск испытывает только
световое давление и поглощает энергию.
Для разрешения проблемы, по нашему мнению,
следует использовать концепцию классического
спина электродинамики, который описывается
некоторой тензорной плотностью 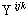 [12 - 17]. Таким образом,
мы должны принять, что классическая
электродинамика не полна. Пондеромоторное
воздействие на элемент поверхности
[12 - 17]. Таким образом,
мы должны принять, что классическая
электродинамика не полна. Пондеромоторное
воздействие на элемент поверхности 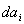 состоит
из силы и вращающего момента.
состоит
из силы и вращающего момента.
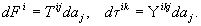
Этот вращающий момент закручивает центральный
диск. Одновременно максвелловские силы снабжают
орбитальным моментом импульса кольцо. В
результате оказывается, что суммарный, спиновый
плюс орбитальный, момент импульса, содержащийся
в луче круговой поляризации и получаемый
мишенью, равен удвоенной величине,
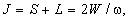
где W √ величина энергии.
Примечание
Материал этой заметки был отклонен или
проигнорирован следующими журналами (в скобках
указана дата подачи материла): Phys. Rev. D (25.09.01),
Foundation of Physics (28.05.01), American J. of Physics (15.09.99, 10.09.01, 28.03.02,
21.06.02), Acta Physica Polonica B (28.01.02, 09.05.02), Письма в ЖЭТФ
(14.05.98), ЖЭТФ (27.01.99, 25.02.99, 13.04.00,
25.05.00, 16.0501, 26.11.01), ТМФ (29.04.99,
17.02.00, 29.05.00, 18.10.00), УФН (25.02.99,
12.01.00, 31.05.00), Физика (18.05.99, 15.10.99,
01.03.00, 25.05.00, 31.05.01, 24.11.01).
Материал этой заметки отклонялся arXiv▓ом (21.01.02, 18.02.02, 02.06.02, 13.06.02).
Список литературы
- Khrapko R.I. Does plane wave not carry a spin? // American Journal of Physics. √
2001, 69.- c.405.
- Гайтлер В. Квантовая теория излучения. √ М.:
ИЛ, 1956.- 451 с.
- Соколов И. // Успехи Физических Наук. √ 1991, ╧ 10.-
с.175.
- Shapochnikov K. // Ann. der Phys. √ 1914, 43.- p.473.
- Humblet J. // Physica. √ 1943, 10.- p.585.
- Crichton J. et al. // General Relativity and Gravitation. √ 1990, 22.-
p.61.
- Ohanian H.C. What is spin? // American Journal of Physics. √ 1986, 54.-
p.500.
- Джексон Д. Классическая электродинамика. - М.:
Мир, 1965.- 524 с.
- Фейнман Р. и др. Фейнмановские лекции по
физике. Т. 8,9. - М.: Мир, 1978. - 524 c.
- Allen L., Padgett M.J. Does a plane wave carry spin angular momentum? // American
Journal of. Physics. √ 2002, 70.- p.567.
- Yurchenko V.B. Does plane wave not carry a spin? // American Journal of Physics.
√ 2002, 70.- p.568
- Храпко Р.И. Истинные тензоры энергии-импульса
и спина среды однозначны.// Теоретические и
экспериментальные проблемы общей теории
относительности и гравитации. Х Российская
гравитационная конференция, Владимир. 1999: Тез.
докл. - Москва, 1999. - с.47.
- R.I. Khrapko. True energy-momentum tensor are unique. Electrodynamics spin tensor
is not zero. √ http://ru.arxiv.org/abs/physics/0102084.
- R.I. Khrapko. Violation of the gauge equivalence. √
http://ru.arxiv.org/abs/physics/0105031.
- Р.И. Храпко. Истинный тензор
энергии-импульса однозначен. - http://www.mai.ru Труды
МАИ, вып. 2.
- Р.И. Храпко. Плотность спина
электромагнитных волн. - http://www.mai.ru Труды МАИ, вып.3
- Р.И. Храпко. Спиновый момент
импульса дипольного излучения. - http://www.mai.ru Труды
МАИ, вып. 6.
Сведения об авторе
Храпко Радий Игоревич, доцент кафедры физики
Московского авиационного
института (государственного технического университета), к.ф.-м.н.
Адрес: 121433, Москва, Б. Филевская, 43 √ 92
Телефон: 144-6312
E-mail: khrapko_ri@hotmail.com
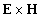 , и, соответственно,
плотность импульса направлены вдоль этого
направления [2 √ 8]. Однако на периферии реальной
световой волны с конечным поперечным сечением,
там, где интенсивность полей уменьшается,
существуют составляющие векторов E и H,
напрвленные вдоль распространения волны, а
, и, соответственно,
плотность импульса направлены вдоль этого
направления [2 √ 8]. Однако на периферии реальной
световой волны с конечным поперечным сечением,
там, где интенсивность полей уменьшается,
существуют составляющие векторов E и H,
напрвленные вдоль распространения волны, а 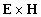 имеет
составляющую, перпендикулярную направлению
распространения. В результате, на периферии
световой волны, то есть на поверхности луча,
локализован момент импульса
имеет
составляющую, перпендикулярную направлению
распространения. В результате, на периферии
световой волны, то есть на поверхности луча,
локализован момент импульса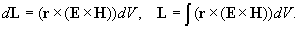
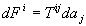 дает силу,
действующую на инфинитезимальную площадку
дает силу,
действующую на инфинитезимальную площадку 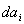 . Согласно
этому выражению, центральная часть мишени, на
которую падает внутренность луча, будет
испытывать световое давление и не будет
испытывать касательных сил, потому что поток
импульса в центральной части луча направлен
перпендикулярно мишени. Внешняя часть мишени, на
которую падает поверхность луча, будет
испытывать касательные силы, поскольку в районе
поверхности луча вектор Пойнтинга имеет
касательную к мишени составляющую. Эти
касательные силы и сообщают мишени упомянутый
момент импульса.
. Согласно
этому выражению, центральная часть мишени, на
которую падает внутренность луча, будет
испытывать световое давление и не будет
испытывать касательных сил, потому что поток
импульса в центральной части луча направлен
перпендикулярно мишени. Внешняя часть мишени, на
которую падает поверхность луча, будет
испытывать касательные силы, поскольку в районе
поверхности луча вектор Пойнтинга имеет
касательную к мишени составляющую. Эти
касательные силы и сообщают мишени упомянутый
момент импульса.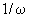 . Это означает, что
центральный диск мишени, получающий энергию и
световое давление, будет получать и спиновый
момент импульса, не описываемый теорией
Максвелла, и будет закручиваться, вопреки
вышеприведенному рассуждению. Такой вывод
следует и из простого рассуждения Р. Фейнмана,
который рассказывает, как световая волна
круговой поляризации передает вращающий момент
поглощающей среде [
. Это означает, что
центральный диск мишени, получающий энергию и
световое давление, будет получать и спиновый
момент импульса, не описываемый теорией
Максвелла, и будет закручиваться, вопреки
вышеприведенному рассуждению. Такой вывод
следует и из простого рассуждения Р. Фейнмана,
который рассказывает, как световая волна
круговой поляризации передает вращающий момент
поглощающей среде [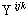 [
[