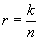 .
.УДК 621.376.57
Способ оценки эффективности блоковых кодов при передаче информации по каналу связи.
А.В.Чикин, А.Г.Зимин, И.А.Ионов.
В статье рассматривается способ сравнения блоковых кодов по критерию качества передачи информации в двоичном симметричном канале без памяти. Для этого вводится в рассмотрение понятие "эффективной скорости" прохождения информации по каналу. Получены точные значения "эффективной скорости" для некоторых блоковых кодов.
Введение.
При проектировании новой системы связи возникает задача выбора наиболее эффективного способа помехоустойчивого кодирования информации для достижения максимальной достоверности ее передачи. Одним из наиболее хорошо проработанных и распространенных методов повышения помехоустойчивости является помехоустойчивое кодирование сообщений в каналах связи. Среди большого разнообразия кодов [1,4] можно выделить один наиболее широкий класс √ блоковые коды. Это √ коды Хэмминга, циклические, БЧХ, с многократным повторением и т.п. Блоковые коды, как правило, состоят из набора символов, связанных между собой определенными линейными или нелинейными соотношениями. За счет этой связи возможно обнаружение и исправление ошибок. Блоковые коды характеризуются, в основном, тремя параметрами: длиной кодовой комбинации, выраженной в количестве символов, √ n; длиной информационной части в одной кодовой комбинации, также выраженной в количестве символов, √ k; и минимальным расстоянием Хэмминга в метрике пространства кода √ d, определяющим минимальный вес двух разрешенных кодовых комбинаций. Как правило, параметр d характеризует обнаруживающую и исправляющую способность кода. Например, в простейших блоковых кодах количество обнаруживаемых кодом ошибок √ d, а количество исправляемых √ (d-1)/2. При описании код записывают как (n,k,d) или (n,k). Скорость кода есть отношение количества информационных бит к длине кодовой комбинации
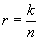 .
.
Очевидно, что для безызбыточного кода r = 1.
При прохождении по каналу связи кодовые комбинации неизбежно могут подвергаться воздействию помехи, и тогда в них будут возникать ошибки. При сравнении между собой различных способов кодирования будем считать, что канал связи, в котором передаются кодовые комбинации, является двоичным симметричным каналом без памяти (ДСК), т.е. ошибки в канале независимы и вероятность ошибки на символ p есть параметр канала.
В этой работе рассматривается метод сравнения различных способов помехоустойчивого блокового кодирования по критерию качества прохождения информационной части по каналу связи. Для этого используется понятие эффективной скорости передачи информации. Под эффективной скоростью передачи понимается средняя скорость прохождения информации по каналу связи до момента ее приема с вероятностью ошибки, равной нулю. В первой части статьи рассматривается методика определения эффективной скорости передачи информации для заданного способа кодирования. Во второй части рассматривается применение полученной эффективной скорости для сравнения между собой различных способов кодирования по выбранному критерию качества передачи информации. В заключении дается оценка выводам, полученным в первом и втором разделе, и практические рекомендации.
Методика определения "эффективной скорости" кодов.
Пусть канал, в котором передаются кодовые комбинации, является двоичным симметричным каналом без памяти (ДСК) с параметром р и требуется передать по каналу связи двоичную информационную последовательность, состоящую из l символов. Перед передачей вся информационная последовательность разбивается на NБЛ = l / k блоков (NБЛ округляется до ближайшего максимального целого) и каждый информационный блок кодируется выбранным кодом (k √ размер информационной части одной кодовой комбинации выбранного кода). За одну передачу передаются все NБЛ кодовых комбинаций. Если после процедуры декодирования на приемной8 стороне принятая информационная последовательность не соответствует передаваемой, то в канале обратной связи посылается специальный сигнал о повторе передачи. Таким образом, количество повторов передачи, произведенных до правильного приема информационной последовательности на приемной стороне (событие А) примем равным m. Вероятность того, что до наступления события А будет произведено ровно m повторов передачи сообщения, будет распределена по "геометрическому+1" закону [2] :
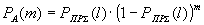 , (1.1)
, (1.1)
где 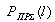 есть вероятность
правильного приема всей
информационной
последовательности, т.е.
вероятность того, что в каждой из NБЛ кодовых
комбинаций не произойдет более t ошибок, равное
исправляющей способности
выбранного кода.
есть вероятность
правильного приема всей
информационной
последовательности, т.е.
вероятность того, что в каждой из NБЛ кодовых
комбинаций не произойдет более t ошибок, равное
исправляющей способности
выбранного кода. 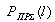 будет зависеть от
количества кодовых комбинаций, т.е.
от NБЛ.
Математическое ожидание величины PA(m) равно 1/
будет зависеть от
количества кодовых комбинаций, т.е.
от NБЛ.
Математическое ожидание величины PA(m) равно 1/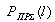 .
Под математическим
ожиданием PA(m) будем понимать
среднее количество повторений
передачи сообщения до тех пор, пока
не произойдет событие А.
.
Под математическим
ожиданием PA(m) будем понимать
среднее количество повторений
передачи сообщения до тех пор, пока
не произойдет событие А.
Теперь, эффективная скорость прохождения информации по каналу связи будет равна
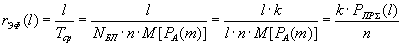 .
.
Физическая интерпретация эффективной скорости есть отношение времени (в битах), затрачиваемого на передачу некодированной информационной последовательности по каналу в отсутствии помех, к среднему2 времени, которое требуется затратить на передачу информационной последовательности по реальному каналу. Чем выше эффективная скорость передачи, тем лучше данный блоковый код приспособлен для переноса информации в данном канале. Максимальное значение rЭФ(l) равно 1 и соответствует случаю безызбыточного кода при отсутствии помех.
Вероятность 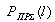 есть
есть
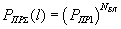 ,
,
где РПР1 вычисляется как
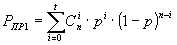 ,
,
где 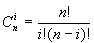 √ число возможных
сочетаний ошибок на длине одной
кодовой комбинации выбранного
блокового кода.
√ число возможных
сочетаний ошибок на длине одной
кодовой комбинации выбранного
блокового кода.
Будем считать, что в обратном канале связь идеальна. Этот канал вводится из теоретических соображений специально для обоснования методики сравнения.
Необходимо отметить, что возможен и другой способ получения значения "эффективной скорости" передачи, который в данной работе не рассматривается. В этом случае рассчитывается среднее время, затраченное на передачу одного информационного блока. Тогда событие А будет заключаться в правильном приеме только одного информационного блока и формула (1.1) будет записана следующим образом
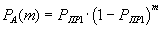 .
.
А формула для "эффективной скорости" передачи информационной последовательности будет выглядеть как
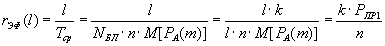 ,
,
т.е. не зависеть от длины информационной последовательности, что обусловлено свойствами выбранного канала ДСК.
Пример 1. Рассмотрим, в качестве примера, безызбыточный код (4,4,0), циклический код (15,4,8), код Хэмминга (7,4,3) и трехкратное повторе2ние с последующим мажоритарным декодированием (12,4,9). Все эти коды имеют одинаковую информационную часть k = 4, поэтому NБЛ будет равно 1.
Запишем для каждого кода вероятность правильного приема.
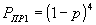
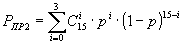
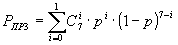
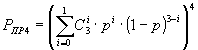 .
.
Подставим полученные выражения в формулу эффективной скорости и результаты отразим в виде зависимостей "эффективной" скорости от вероятности ошибки на символ в канале, см. рис.1
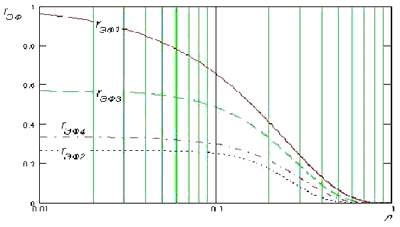
Рис.1
rэф1 √ rэф4 √ обозначены "эффективные" скорости безызбыточного, циклического (15,4), Хэмминга (7,4) и кода с повторениями (12,4), соответственно.
Из приведенной зависимости видно, что при равных условиях выгоднее использовать безызбыточный код. Циклический же код (15,4), несмотря на то, что в нем добавлено большое количество избыточности и обладает высокой корректирующей способностью, проигрывает.
Пример 2. В качестве второго примера, рассмотрим безызбыточный код, циклический код (21,11,6), циклический код (15,4,8), циклический код (15,7,5), код Хэмминга (7,4,3), трехкратное повторение с последующим мажоритарным декодированием, пятикратное повторение с последующим мажоритарным декодированием, циклический код (15,11,3).
Формулы вероятности правильного приема информационной части сообщения и эффективной скорости для каждого способа кодирования сведем в таблицу табл.1.
Табл. 1
| Способ кодирования | Вероятность
правильного приема информационной части
сообщения, 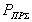 |
| Безызбыточный | 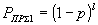 |
| Циклический код (21,11) | 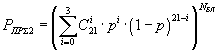 |
| Циклический код (15,4) | 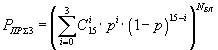 |
| Циклический код (15,7) | 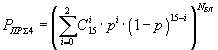 |
| Код Хэмминга (7,4) | 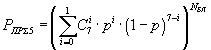 |
| 3-х кратное повторение | 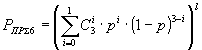 |
| 5-ти кратное повторение | 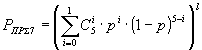 |
| Циклический код (15,11,3) | 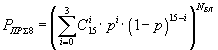 |
Подставим полученные выражения в формулу "эффективной" скорости и результаты отразим в виде зависимостей "эффективной" скорости от вероятности ошибки на символ в канале, см. рис. 2 при l = 512 бит, см. рис 3 при l = 9600 бит.
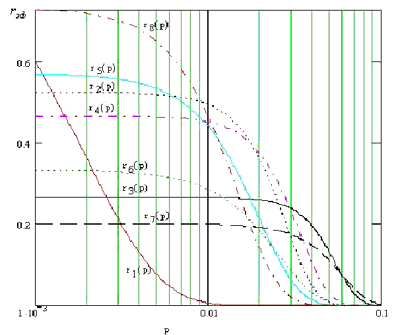
Рис. 2
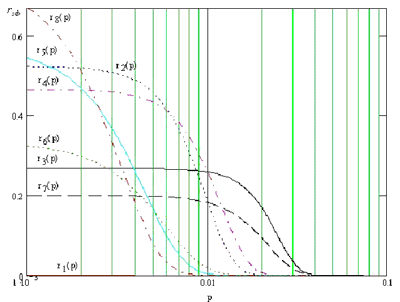
Рис. 3
Анализируя приведенные зависимости, нельзя еще дать однозначного ответа какой способ кодирования выгоднее использовать. Действительно, по графикам видно, что один способ кодирования позволяет работать при довольно большой вероятности ошибки на символ в канале, но с низк2ой электрической скоростью передачи; другой √ позволяет работать при более высокой электрической скорости передачи, но только при малых величинах вероятности ошибки на символ и т.д. К тому же, очевидно, что решающую роль играет длина информационной последовательности. С увеличением длины информационной последовательности происходит как бы смещение всей картинки в область малых значений вероятности ошибки на символ.
Определение критерия качества передачи информационного блока при выбранном способе кодирования.
Очевидно, что критерий качества будет зависеть не только от длины информационного блока, но и от характеристик канала, в котором происходит передача.
Будем считать, что канал, в котором происходит передача, является гауссовским каналом и передача осуществляется фазовой манипуляцией на 180° , тогда вероятность ошибки на символ
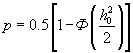 ,
,
где h02 √есть отношение
сигнал√шум в канале, а Ф(·) √
есть интеграл вероятности.
Соответствующая формула для других
способов модуляции может быть
найдена в [3] . При значениях р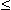 0.1
эта формула может быть
аппроксимирована следующим
выражением
0.1
эта формула может быть
аппроксимирована следующим
выражением
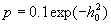 .
.
Будем считать, что
при заданной вероятности ошибки на
символ в канале качество способа
кодирования есть произведение его
эффективной скорости rЭФ(l) на отношение
сигнал√шум h02 с некоторым весом 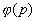 .
Далее для упрощения
будем считать, что все значения
сигнал/шум равновероятны и
.
Далее для упрощения
будем считать, что все значения
сигнал/шум равновероятны и 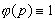 . Тогда
проинтегрировав это произведение
по всем значениям вероятностей
ошибок в канале, получим адекватный
критерий качества К(l) выбранного способа
кодирования.
. Тогда
проинтегрировав это произведение
по всем значениям вероятностей
ошибок в канале, получим адекватный
критерий качества К(l) выбранного способа
кодирования.
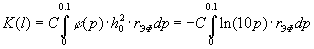 ,
,
где С √
нормировочная константа,
выбираемая из условия 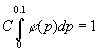 .
.
И, затем сравнивая между собой полученные значения K(l), можно выбрать наиболее эффективный код по данному критерию из совокупности рассматриваемых способов кодирования.
Пример 3. Сравним по полученному критерию качества К(l) безызбыточный код, циклический код (21,11,6), циклический код (15,4,8), циклический код (15,7,5), код Хэмминга (7,4,3), трехкратное повторение с последующим мажоритарным декодированием, пятикратное повторение с последующим мажоритарным декодированием, циклический код (15,11,3), циклический код (63,36,10) для l=4; 64; 512; 2048; 9600 бит. Результаты сведем в табл. 2.
Табл.2.
| Способ кодирования | l = 4 | l = 64 | l = 512 | l = 2048 | l = 9600 | |
| 1 | Безызбыточный | 0.091 | 0.038 | 0.009 | 0.003 | 7·10-4 |
| 2 | Циклический код (21,11) | 0.05 | 0.043 | 0.031 | 0.022 | 0.016 |
| 3 | Циклический код (15,4) | 0.027 | 0.026 | 0.022 | 0.018 | 0.015 |
| 4 | Циклический код (15,7) | 0.046 | 0.041 | 0.03 | 0.023 | 0.016 |
| 5 | Код Хэмминга (7,4) | 0.056 | 0.045 | 0.026 | 0.016 | 9·10-3 |
| 6 | 3-х кратное повторение | 0.033 | 0.028 | 0.018 | 0.011 | 6·10-3 |
| 7 | 5-х кратное повторение | 0.02 | 0.019 | 0.017 | 0.014 | 0.01 |
| 8 | Циклический код (15,11) | 0.068. | 0.052 | 0.028 | 0.017 | 9·10-3 |
| 9 | Циклический код (63,36) | 0.052 | 0.049 | 0.038 | 0.031 | 0.024 |
Подчеркнуты максимальные значения критерия качества.
На рис.4 приводится зависимость критерия качества К(l) вышеуказанных кодов от длины информационного блока l.
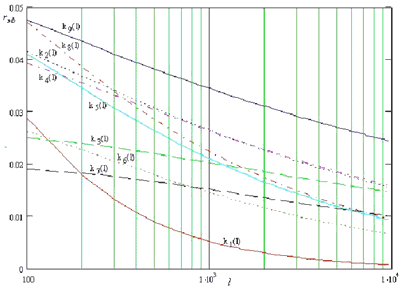
Рис.4.
Заключение.
Анализируя вышеприведенную зависимость, можно сделать однозначный вывод, что сравнение различных способов кодирования по выбранному критерию нужно проводить не только исходя из знания параметров канала связи, но и учитывая длину передаваемой информационной последовательности. Действительно, с увеличением длины информационной последовательности, способ кодирования, который ранее давал лучшие результаты, теперь может проигрывать.
Также нужно отметить, что с увеличением длины
информационного блока, выгоднее
использовать длинные коды со
скоростью примерно 1/2 при весовой
функции 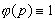 .
.
Список литературы.
Сведения об авторах
Чикин Алексей Викторович, аспирант кафедры радиосистем передачи информации и управления Московского авиационного института (государственного технического университета)
E-mail: avchikin@yandex.ru
Зимин Андрей Геннадьевич, аспирант кафедры радиосистем передачи информации и управления Московского авиационного института (государственного технического университета)
E-mail: andrew@javad.ru
Ионов Игорь Александрович, с.н.с. TPS, к.т.н.
E-mail: igor@javad.ru