Алгоритм поиска на перестановочном множестве базируется на следующих теоретических соображениях. Задача определения оптимальной очередности запуска деталей относится к группе перестановочных задач комбинаторного программирования [2] , множество решений которых представляет собой так называемый перестановочный многогранник, то есть векторную решетку с возможностью перехода в любое решение за конечное число перестановок. Перестановочный многогранник является матроидом √ комбинаторным множеством, на котором имеет место совпадение локального и глобального оптимумов целевых функций определенного вида. Для того, чтобы локальный и глобальный экстремумы целевой функции совпадали на матроиде, эта функция должна быть дискретно-выпуклой. Дискретно-выпуклой называют функцию дискретных переменных, обладающую свойствами, аналогичными свойству выпуклости целевой функции непрерывных экстремальных задач. На матроиде может быть введено понятие градиента дискретно-выпуклой функции и на его основе получено конструктивное условие экстремума. Для решения в этом случае используют алгоритмы, аналогичные алгоритмам градиентных методов решения непрерывно-экстремальных задач. Эти алгоритмы характеризуются временем сходимости, на порядки превышающим это время для переборных (универсальных точных) методов решения.

Для зависимости суммарной продолжительности цикла работ от порядка их выполнения на рабочих местах, по всей вероятности, не представляется возможным аналитически доказать ее дискретную выпуклость ввиду параллельности обработки партий деталей одной номенклатуры на разных рабочих местах и включения в продолжительность цикла работ разовых и регулярных профилактических ремонтов. Поэтому в предлагаемом комбинаторном методе оптимизации расписания работы рабочих мест решения, полученные в результате поиска по перестановочному многограннику подвергаются дальнейшему улучшению по алгоритму метода ветвей и границ (хотя такое улучшение может оказаться и ненужным). Процедура поиска на перестановочном многограннике повторяется несколько раз с различными отправными точками и далее наилучший из полученных вариантов используется в качестве начального решения в алгоритме метода ветвей и границ.

Для реализации перестановочного алгоритма на множестве решений задачи вводится понятие окрестности точки, в качестве которого выступает множество комбинаций перестановок, которые могут быть получены из рассматриваемой за одну транспозицию, то есть за одну перемену местами двух произвольных операций. В окрестности точки ищется перестановка с наилучшим значением целевой функции задачи, которая затем принимается в качестве следующего анализируемого варианта (следующей точки поиска). Поскольку определить число локальных минимумов задачи не представляется возможным, число реализаций поиска по перестановочному многограннику ограничивается заданным числом попыток.

Для математической реализации предложенной схемы поиска вектор решения задачи представляется в виде

(x₁ , x₂ , x₃ ,┘., x_i ,┘.., x_n)      (5)

где x_i √ соответствует номеру партии деталей, помещаемой в i-ю по номеру очередь.

Таким образом, x_i может принимать значения от 1 до n:

x_i {1,2,┘.,n}, i=1,┘,n      (6)

где n √ общее число партий деталей, запускаемых в обработку.

Допустимость решения при этом регламентируется условием

( x_i x_k , k=1,┘,n, k i ), i=1,┘n      (7)

Алгоритм поиска на перестановочном множестве включает в себя следующую последовательность действий.

1. Начальное значение вектора Х¹ выбирается как наилучшее среди полученных решений, полученных по алгоритму случайного поиска.

2. Для Х¹, отражающего очередность деталей на рабочих местах, рассчитываются времена начала запуска посредством последовательного применения выражения (2) (или (3) √ в зависимости от постановки задачи) для каждого номера очереди (i=1,┘,n) по каждому из рабочих мест (j=1,┘,m).

3. На основании полученного расписания запуска партий деталей по рабочим местам рассчитывается общая продолжительность производственного цикла по формуле (1), которая принимается в качестве значения целевой функции задачи k-го шага поиска F^k.

4. Организуется просмотр окрестности анализируемого решения как циклический перебор всех элементов вектора Х^k и просмотр для каждого из этих элементов всех возможных его перестановок с другими элементами. Для каждой из анализируемых перестановок рассчитывается свое значение целевой функции задачи по по формуле (1).

Если в процессе обзора окрестности решения Х^k удается получить значение F, лучшее, чем F^k , то происходит переход к пункту 5. алгоритма.

Если в результате просмотра окрестности точки Х^k не удается обнаружить точку со значением функции лучше, чем F^k , то F^k принимается в качестве рекордного значения целевой функции F^R , Х^k √ в качестве рекордного решения Х^R и происходит переход к пункту 6.

5. Данная точка окрестности точки Х^k принимается в качестве решения следующего шага поиска Х^k+1 , а значение F в данной точке окрестности √ в качестве значения целевой функции в (k+1)-й точке поиска - F^k+1 ; осуществляется возврат к пункту 4.

6. Если заданное число попыток реализации поиска на перестановочном множестве еще не реализовано, осуществляется переход к пункту 1., в противном случае поиск переходит в новую стадию √ применению алгоритма метода ветвей и границ √ к пункту 7.

7. Для полученного на предыдущем этапе поиска рекордного решения производится расчет оценок снизу всех соответствующих Х^R частичных решений уровней от 1 до n-1 , то есть частичных решений:

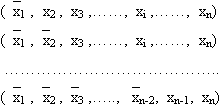    (8)

Расчет оценок снизу целевой функции задачи производится по формуле:

    (9)

где t_l^√(j,j-1)- смещение по началу обработки партии деталей номенклатуры l на (i-1)-м подающем и j-м получающем рабочих местах.

t_l^+(j,j-1)- смещение по окончанию обработки партии деталей номенклатуры l на (i-1)-м подающем и j-м получающем рабочих местах.

Такая оценка снизу несколько оптимистична, но она позволяет гарантировать, что в процессе поиска не произойдет необоснованного отсечения решений, среди которых может оказаться и оптимальное.

Применяемая далее схема метода ветвей и границ несколько специфична, ввиду специфичности множества решений перестановочной задачи, изображенного на рисунке 2, из которого видно, что число ветвлений на каждом из уровней дерева уменьшается на единицу и соответственно на предпоследнем уровне уже нет альтернативных продолжений анализируемого частичного решения (на рисунке 2 показано дерево решений для трех партий деталей).  

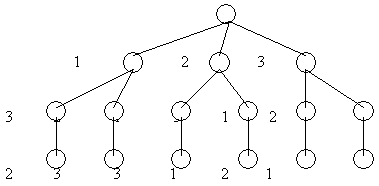
Рис. 2. Дерево решений перестановочных задач.

После получения оценок снизу для всех частичных решений, соответствующих рекордному полному решению, полученному на этапе применения перестановочного алгоритма, происходит подъем от конечной вершины дерева решений к вершине уровня n-2, то есть переход к частичному решению . Если полученная ранее оценка снизу этого уровня меньше, чем имеющийся рекорд, это частичное решение достраивается до второго производного от него полного решения. Для этого полного решения определяется значение целевой функции F, и если F< F^R, то F^R присваивается значение F, а полученное полное решение принимается в качестве нового рекордного решения Х^R.

Далее осуществляется подъем к частичному решению уровня и если полученная ранее оценка этого уровня меньше, чем имеющийся рекорд, это частичное решение достраивается до очередного частичного решения уровня , для этого частичного решения рассчитывается его оценка снизу, и так далее.